
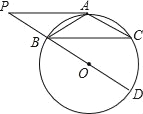
【題目】如圖,⊙O中,點A為![]() 中點,BD為直徑,過A作AP∥BC交DB的延長線于點P.
中點,BD為直徑,過A作AP∥BC交DB的延長線于點P.
(Ⅰ)求證:PA是⊙O的切線;
(Ⅱ)若BC=2![]() ,AB=2
,AB=2![]() ,求sin∠ABD的值.
,求sin∠ABD的值.
【答案】(1)見解析;(2)![]()
【解析】分析:(Ⅰ)根據垂徑定理得出AO⊥BC,進而根據平行線的性質得出AP⊥AO,即可證得結論;
(Ⅱ)根據垂徑定理得出BE=![]() ,在Rt△ABE中,利用銳角三角函數關系得出sin∠BAE=
,在Rt△ABE中,利用銳角三角函數關系得出sin∠BAE=![]() ,再根據等腰三角形的性質得出∠ABD=∠BAE,即可求得求sin∠ABD=sin∠BAE=
,再根據等腰三角形的性質得出∠ABD=∠BAE,即可求得求sin∠ABD=sin∠BAE=![]() .
.
詳解:(Ⅰ)證明:連結AO,交BC于點E.
∵點A是![]() 的中點
的中點
∴AO⊥BC,
又∵AP∥BC,
∴AP⊥AO,
∴AP是⊙O的切線;
(Ⅱ)解:∵AO⊥BC,BC=2![]() ,
,
∴BE=![]() BC=
BC=![]() ,
,
又∵AB=6
∴sin∠BAE=![]() ,
,
∵OA=OB
∴∠ABD=∠BAO,
∴sin∠ABD=sin∠BAE=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
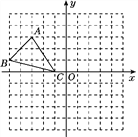
【題目】如圖,已知網格上最小的正方形的邊長為1.
(1)分別寫出A,B,C三點的坐標;
(2)作△ABC關于y軸的對稱圖形△A′B′C′(不寫作法),想一想:關于y軸對稱的兩個點之間有什么關系?
(3)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O在直線AB上,OC、OD是兩條射線,OC⊥OD,射線OE平分∠BOC.
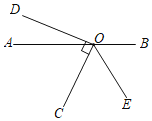
(1)若∠DOE=150°,求∠AOC的度數.
(2)若∠DOE=α,則∠AOC= .(請用含α的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的圖象如圖,下列四個結論:
的圖象如圖,下列四個結論:
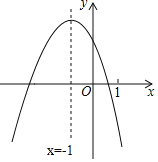
![]() ;
;
![]() ;
;
![]() 關于x的一元二次方程
關于x的一元二次方程![]() 沒有實數根;
沒有實數根;
![]() 為常數
為常數![]() .
.
其中正確結論的個數是![]()
![]()
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知О是直線AB上的一點,![]() ,OE平分
,OE平分![]() .
.
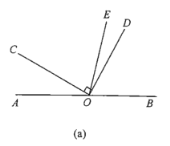
(1)在圖(a)中,若![]() ,求
,求![]() 的度數;
的度數;
(2)在圖(a)中,若![]() ,直接寫出
,直接寫出![]() 的度數(用含
的度數(用含![]() 的代數式表示)
的代數式表示)
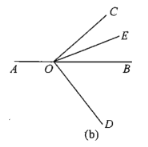
(3)將圖(a)中的![]() 繞頂點O順時針旋轉至圖(b)的位置.
繞頂點O順時針旋轉至圖(b)的位置.
①探究![]() 和
和![]() 的度數之間的關系,直接寫出結論;
的度數之間的關系,直接寫出結論;
②在![]() 的內部有一條射線OF,滿足:
的內部有一條射線OF,滿足:![]() ,試確定
,試確定![]() 與
與![]() 的度數之間的關系,并說明理由.
的度數之間的關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點O是AB上的一點,∠COE=90°,OF平分∠AOE.
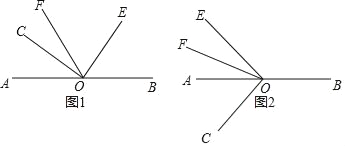
(1)如圖1,當點C,E,F在直線AB的同一側時,若∠AOC=40°,求∠BOE和∠COF的度數;
(2)在(1)的條件下,∠BOE和∠COF有什么數量關系?請直接寫出結論,不必說明理由;
(3)如圖2,當點C,E,F分別在直線AB的兩側時,若∠AOC=β,那么(2)中∠BOE和∠COF的數量關系是否仍然成立?請寫出結論,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com