
【題目】閱讀、思考、解決問題:
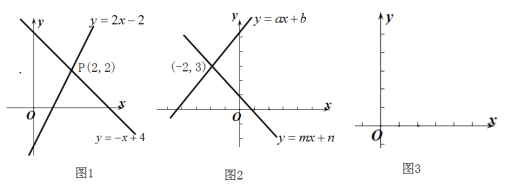
(1)如圖(1)兩個函數![]() 和
和![]() 的圖象交于點
的圖象交于點![]() ,
,![]() 的坐標
的坐標![]() 是否滿足這兩個函數式?即
是否滿足這兩個函數式?即![]() 是方程
是方程![]() 的解嗎?是方程
的解嗎?是方程![]() 的解嗎?答: ① (是、不是)這就是說:函數
的解嗎?答: ① (是、不是)這就是說:函數![]() 和
和![]() 圖象的交點坐標 ② (是、不是)方程組
圖象的交點坐標 ② (是、不是)方程組![]() 的解;反之,方程組
的解;反之,方程組![]() 的解 ③ (是、不是)函數
的解 ③ (是、不是)函數![]() 和
和![]() 圖象的交點坐標.
圖象的交點坐標.
(2)根據圖(2)寫出方程組![]() 的解是:____________
的解是:____________
(3)已知兩個一次函數![]() 和
和![]() .
.
①求這兩個函數圖象的交點坐標;
②在圖(3)的坐標系中畫出這兩個函數的圖象
③根據圖象寫出當![]() 時,
時,![]() 的取值范圍.
的取值范圍.
【答案】(1)是,是,是;(2)![]() ;(3)①(1,4);②見解析;③x>1.
;(3)①(1,4);②見解析;③x>1.
【解析】
(1)根據兩個一次函數圖象的交點坐標與它們組成的二元一次方程組的解之間的關系進行解答即可;
(2)由函數圖象中的交點坐標可得方程組的解;
(3)①求出這兩個函數解析式組成的方程組的解即可;
②根據![]() 過點(0,3),
過點(0,3),![]() 過點(0,1),且這兩個函數圖象的交點坐標為:(1,4)畫出函數圖象即可;
過點(0,1),且這兩個函數圖象的交點坐標為:(1,4)畫出函數圖象即可;
③根據函數圖象,找出![]() 的圖象在
的圖象在![]() 的圖象上方時x的取值范圍即可.
的圖象上方時x的取值范圍即可.
解:(1)如圖(1)兩個函數![]() 和
和![]() 的圖象交于點
的圖象交于點![]() ,
,![]() 的坐標
的坐標![]() 是否滿足這兩個函數式?即
是否滿足這兩個函數式?即![]() 是方程
是方程![]() 的解嗎?是方程
的解嗎?是方程![]() 的解嗎?答:是;這就是說:函數
的解嗎?答:是;這就是說:函數![]() 和
和![]() 圖象的交點坐標是方程組
圖象的交點坐標是方程組![]() 的解;反之,方程組
的解;反之,方程組![]() 的解是函數
的解是函數![]() 和
和![]() 圖象的交點坐標;
圖象的交點坐標;
故答案為:是,是,是;
(2)由圖(2)可得:方程組![]() 的解是:
的解是:![]() ;
;
(3)①聯立![]() ,解得:
,解得:![]() ,
,
∴這兩個函數圖象的交點坐標為:(1,4);
②易得![]() 過點(0,3),
過點(0,3),![]() 過點(0,1),且這兩個函數圖象的交點坐標為:(1,4),函數圖象如圖3所示:
過點(0,1),且這兩個函數圖象的交點坐標為:(1,4),函數圖象如圖3所示:
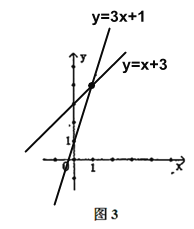
③由函數圖象可得:![]() 時,
時,![]() 的取值范圍是:x>1.
的取值范圍是:x>1.


科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等腰三角形,AB=AC,點D是AB上一點,過點D作DE⊥BC交BC于點E,交CA延長線于點F.
(1)證明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的長,

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在長方形![]() 中,BC=3,動點
中,BC=3,動點![]() 從
從![]() 出發,以每秒1個單位的速度,沿射線
出發,以每秒1個單位的速度,沿射線![]() 方向移動,作
方向移動,作![]() 關于直線
關于直線![]() 的對稱
的對稱![]() ,設點
,設點![]() 的運動時間為
的運動時間為![]()
(1)當P點在線段BC上且不與C點重合時,若直線PB’與直線CD相交于點M,且∠PAM=45°,試求:AB的長
(2)若AB=4
①如圖2,當點B’落在AC上時,顯然△PCB’是直角三角形,求此時t的值
②是否存在異于圖2的時刻,使得△PCB’是直角三角形?若存在,請直接寫出所有符合題意的t的值?若不存在,請說明理由

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2017懷化,第10題,4分)如圖,A,B兩點在反比例函數![]() 的圖象上,C,D兩點在反比例函數
的圖象上,C,D兩點在反比例函數![]() 的圖象上,AC⊥y軸于點E,BD⊥y軸于點F,AC=2,BD=1,EF=3,則
的圖象上,AC⊥y軸于點E,BD⊥y軸于點F,AC=2,BD=1,EF=3,則![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在□ABCD中,![]() ,
,![]() ,
,![]() ,射線AE平分
,射線AE平分![]() 動點P以
動點P以![]() 的速度沿AD向終點D運動,過點P作
的速度沿AD向終點D運動,過點P作![]() 交AE于點Q,過點P作
交AE于點Q,過點P作![]() ,過點Q作
,過點Q作![]() ,交PM于點
,交PM于點![]() 設點P的運動時間為
設點P的運動時間為![]() ,四邊形APMQ與四邊形ABCD重疊部分面積為
,四邊形APMQ與四邊形ABCD重疊部分面積為![]()


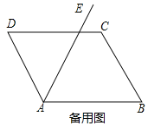
![]() ______
______![]() 用含t的代數式表示
用含t的代數式表示![]()
![]() 當點M落在CD上時,求t的值.
當點M落在CD上時,求t的值.
![]() 求S與t之間的函數關系式.
求S與t之間的函數關系式.
![]() 如圖2,連結AM,交PQ于點G,連結AC、BD交于點H,直接寫出t為何值時,GH與三角形ABD的一邊平行或共線.
如圖2,連結AM,交PQ于點G,連結AC、BD交于點H,直接寫出t為何值時,GH與三角形ABD的一邊平行或共線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,與CD相交于點F,DH⊥BC于H,交BE于G.下列結論:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正確的是
BF;④AE=BG.其中正確的是

A. ①② B. ①③ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
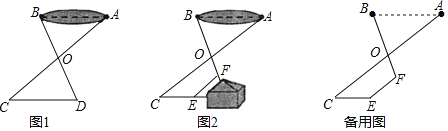
【題目】如圖1,為測量池塘寬度AB,可在池塘外的空地上取任意一點O,連接AO,BO,并分別延長至點C,D,使OC=OA,OD=OB,連接CD
(1)求證:AB=CD;
(2)如圖2,受地形條件的影響,于是采取以下措施:延長AO至點C,使OC=OA,過點C作AB的平行線CE,延長BO至點F,連接EF,測得∠CEF=140°,∠OFE=110°,CE=11m,EF=10m,請直接寫出池塘寬度AB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com