
【題目】如圖1,在長方形![]() 中,BC=3,動點
中,BC=3,動點![]() 從
從![]() 出發(fā),以每秒1個單位的速度,沿射線
出發(fā),以每秒1個單位的速度,沿射線![]() 方向移動,作
方向移動,作![]() 關于直線
關于直線![]() 的對稱
的對稱![]() ,設點
,設點![]() 的運動時間為
的運動時間為![]()
(1)當P點在線段BC上且不與C點重合時,若直線PB’與直線CD相交于點M,且∠PAM=45°,試求:AB的長
(2)若AB=4
①如圖2,當點B’落在AC上時,顯然△PCB’是直角三角形,求此時t的值
②是否存在異于圖2的時刻,使得△PCB’是直角三角形?若存在,請直接寫出所有符合題意的t的值?若不存在,請說明理由

【答案】(1)AB的長為3;(2)①![]() ;②t的值為
;②t的值為![]() 或
或![]() 或4.
或4.
【解析】
(1)如圖所示,延長![]() 與CD交于M,連接AM,用角角邊證明
與CD交于M,連接AM,用角角邊證明![]() ,可推出AB=BC=3.
,可推出AB=BC=3.
(2)①在Rt△![]() 中,找出邊長利用勾股定理建立方程求解;
中,找出邊長利用勾股定理建立方程求解;
②分三種情況討論:![]() ,
,![]() ,
,![]() ,分別作出相應的圖形,在
,分別作出相應的圖形,在![]() 中,分別找出邊長,利用勾股定理建立方程求解.
中,分別找出邊長,利用勾股定理建立方程求解.
(1)如圖所示,延長![]() 與CD交于M,連接AM,
與CD交于M,連接AM,

由折疊的性質可知![]() ,
,![]() ,
,![]()
∵![]() ,
,![]() ,
,
∴![]()
在![]() 和
和![]() 中,
中,

∴![]() ≌
≌![]() (AAS)
(AAS)
∴![]()
又∵ABCD為矩形,∴AD=BC=3,
∴AB=3
(2)①在Rt△ABC中,![]()
∵點P點的運動時間為t,速度為1,∴BP=t,
![]() ,
,![]() ,
,![]() ,
,
在Rt△![]() 中,由勾股定理有
中,由勾股定理有![]() ,即
,即![]() ,解得
,解得![]() .
.
②當![]() ,如下圖所示,
,如下圖所示,

∵四邊形ABCD為矩形,∴AD=BC=3,CD=AB=4,
有折疊性質有![]() ,在Rt△
,在Rt△![]() 中,
中,
![]() ,
,
∴![]()
在Rt△![]() 中,
中,![]() ,
,![]()
![]() ,即
,即![]() ,解得
,解得![]()
當∠![]() =90°時,如下圖所示,
=90°時,如下圖所示,

由折疊可得![]() ,
,
在Rt△![]() 中,
中,![]()
在Rt△![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ,即
,即![]() ,解得
,解得![]()
當![]() =90°時,如下圖所示,根據折疊易得四邊形
=90°時,如下圖所示,根據折疊易得四邊形![]() 為正方形,∴PB=AB=4
為正方形,∴PB=AB=4

綜上,滿足題意的t的值為![]() 或
或![]() 或4.
或4.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,點E, F在直線AC上,DF=BE, ∠AFD=∠CEB,下列條件中不能判斷△ADF≌△CBE的是( )

A.∠D=∠BB.AD=CBC.AE=CFD.AD// BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將平行四邊形紙片ABCD按如圖方式折疊,使點C與A重合,點D落到D′處,折痕為EF.

(1)求證:△ABE≌△AD′F;
(2)連接CF,判斷四邊形AECF是什么特殊四邊形?證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 是第一、三象限的角平分線.
是第一、三象限的角平分線.

(1)由圖觀察易知A(0,2)關于直線l的對稱點A′的坐標為(2,0),請在圖中分別標明B(5,3)、C(-2,5)關于直線l的對稱點B′、C′的位置,并寫出他們的坐標:![]() ___________、
___________、![]() ___________;
___________;
(2)結合圖形觀察以上三組點的坐標,你會發(fā)現:坐標平面內任一點![]() 關于第一、三象限的角平分線
關于第一、三象限的角平分線![]() 的對稱點
的對稱點![]() 的坐標為___________(不必證明);
的坐標為___________(不必證明);
(3)已知兩點![]() 、
、![]() ,試在直線L上畫出點Q,使點Q到D、E兩點的距離之和最小,求QD+QE的最小值.
,試在直線L上畫出點Q,使點Q到D、E兩點的距離之和最小,求QD+QE的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+bx+c與一直線相交于A(﹣1,0),C(2,3)兩點,與y軸交于點N.其頂點為D.

(1)拋物線及直線AC的函數關系式;
(2)設點M(3,m),求使MN+MD的值最小時m的值;
(3)若拋物線的對稱軸與直線AC相交于點B,E為直線AC上的任意一點,過點E作EF∥BD交拋物線于點F,以B,D,E,F為頂點的四邊形能否為平行四邊形?若能,求點E的坐標;若不能,請說明理由;
(4)若P是拋物線上位于直線AC上方的一個動點,求△APC的面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀、思考、解決問題:
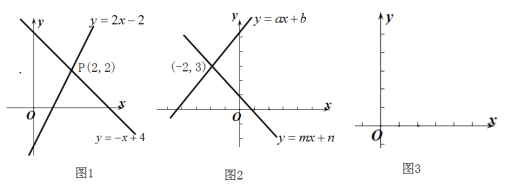
(1)如圖(1)兩個函數![]() 和
和![]() 的圖象交于點
的圖象交于點![]() ,
,![]() 的坐標
的坐標![]() 是否滿足這兩個函數式?即
是否滿足這兩個函數式?即![]() 是方程
是方程![]() 的解嗎?是方程
的解嗎?是方程![]() 的解嗎?答: ① (是、不是)這就是說:函數
的解嗎?答: ① (是、不是)這就是說:函數![]() 和
和![]() 圖象的交點坐標 ② (是、不是)方程組
圖象的交點坐標 ② (是、不是)方程組![]() 的解;反之,方程組
的解;反之,方程組![]() 的解 ③ (是、不是)函數
的解 ③ (是、不是)函數![]() 和
和![]() 圖象的交點坐標.
圖象的交點坐標.
(2)根據圖(2)寫出方程組![]() 的解是:____________
的解是:____________
(3)已知兩個一次函數![]() 和
和![]() .
.
①求這兩個函數圖象的交點坐標;
②在圖(3)的坐標系中畫出這兩個函數的圖象
③根據圖象寫出當![]() 時,
時,![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,∠A=140°,∠D=80°.

(1)如圖1,若∠B=∠C,試求出∠C的度數;
(2)如圖2,若∠ABC的角平分線BE交DC于點E,且BE∥AD,試求出∠C的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于點O,E為AC上一點,且AE=OC.

(1)求證:AP=AO;
(2)求證:PE⊥AO.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com