如圖，E,F分別是□ABCD的邊BA,DC延長線上的點，且AE＝CF，EF交AD于G，交BC于H.
（1）圖中兩對全等的三角形是 ;（不添加任何輔助線）
（2）請在（1）問中選出一對你認為全等的三角形進行證明.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
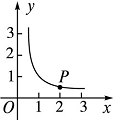
如圖，點P在反比例函數y＝
(x＞0)的圖象上，且橫坐標為2.若將點P先向右平移兩個單位，再向上平移一個單位后所得的像為點P′.則在第一象限內，經過點P′的反比例函數圖象的解析式是( )．
A．y＝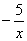
(x＞0) B．y＝
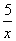(x＞0) C．y＝
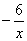(x＞0) D．y＝
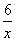(x＞0)
查看答案和解析>>
科目：初中數學 來源： 題型：
已知一個樣本，共100個數據，在頻數分布直方圖中各小長方形的高之比為1∶3∶4∶2，則下列說法錯誤的是( )．
A．頻數最小的一組數據的個數是10
B．數據最多的一組的頻率是4
C．最后一組的數據個數為20
D．第一組的頻率是0.1
查看答案和解析>>
科目：初中數學 來源： 題型：
操作：小明準備制作棱長為1cm的正方體紙盒，現選用一些廢棄的紙片進行如下設計：
 | |||
 | |||
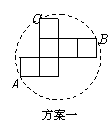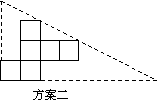紙片利用率=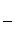
×100%
發現：（1）方案一中的點A.B恰好為該圓一直徑的兩個端點．你認為小明的這個發現是否正確，請說明理由．
（2）小明通過計算，發現方案一中紙片的利用率僅約為38.2%．請幫忙計算方案二的利用率，并寫出求解過程．
探究：（3）小明感覺上面兩個方案的利用率均偏低，又進行了新的設計（方案三），請直接寫出方案三的利用率．
|
 |
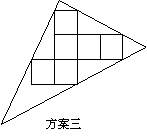查看答案和解析>>
科目：初中數學 來源： 題型：
閱讀材料：
對于平面內的任意兩點A（x1，y1），B（x2，y2），
由勾股定理易知A、B兩點間的距離公式為：
AB＝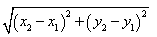
．
如：已知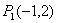
，
，
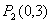則
解答下列問題：
已知點E（6，10），F（0，2），C（0，1）。
（1）直接應用平面內兩點間距離公式計算，
E、F之間的距離為_ _5及代數式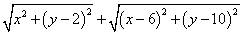
的最小值為 ；
（2）求以C為頂點，且經過點E的拋物線的解析式；
（3）①若點D是上述拋物線上的點，且其橫坐標為 -3，試求DF的長；
②若點P是該拋物線上的任意一點，試探究線段FP的長度與點P縱坐標的數量關系，并證明你的猜想。
③我們知道“圓可以看成是所有到定點的距離等于定長的點的集合”。類似地，拋物線可以看成是_______________________________________．
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的
頂點坐標是（ ）
