
如圖,點![]() 、
、![]() 、
、![]() 、
、![]() 在同一直線上,點
在同一直線上,點![]() 和點
和點![]() 分別在直線
分別在直線![]() 的兩側,且
的兩側,且![]() ,
,![]() ,
,![]() .
.
(1)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)若![]() ,
,![]() ,
,![]() ,
,
當![]() 為何值時,四邊形
為何值時,四邊形![]() 是菱形.
是菱形.
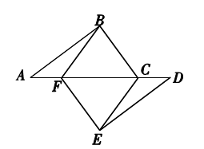
考點:相似三角形的判定與性質;全等三角形的判定與性質;勾股定理;平行四邊形的判定;菱形的判定。
解答:(1)證明:∵AF=DC,∴AF+FC=DC+FC,即AC=DF.
在△ABC和△DEF中,
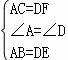 ,
,
∴△ABC≌DEF(SAS),
∴BC=EF,∠ACB=∠DFE,∴BC∥EF,
∴四邊形BCEF是平行四邊形.
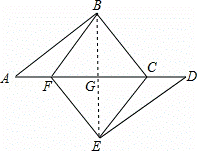
(2)解:連接BE,交CF與點G,
∵四邊形BCEF是平行四邊形,
∴當BE⊥CF時,四邊形BCEF是菱形,
∵∠ABC=90°,AB=4,BC=3,
∴AC=![]() =5,
=5,
∵∠BGC=∠ABC=90°,∠ACB=∠BCG,
∴△ABC∽△BGC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴CG=
,∴CG=![]() ,
,
∵FG=CG,∴FC=2CG=![]() ,
,
∴AF=AC﹣FC=5﹣![]() =
=![]() ,
,
∴當AF=![]() 時,四邊形BCEF是菱形.
時,四邊形BCEF是菱形.


科目:初中數學 來源: 題型:
 3、如圖,地面上有不在同一直線上的A,B,C三點,一只青蛙位于地面異于A,B,C的P點,第一步青蛙從P跳到P關于A的對稱點P1,第二步從P1跳到P1關于B的對稱點P2,第三步從P2跳到P2關于C的對稱點P3,第四步從P3跳到P3關于A的對稱點P4…以下跳法類推,青蛙至少跳幾步回到原處P.( )
3、如圖,地面上有不在同一直線上的A,B,C三點,一只青蛙位于地面異于A,B,C的P點,第一步青蛙從P跳到P關于A的對稱點P1,第二步從P1跳到P1關于B的對稱點P2,第三步從P2跳到P2關于C的對稱點P3,第四步從P3跳到P3關于A的對稱點P4…以下跳法類推,青蛙至少跳幾步回到原處P.( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com