
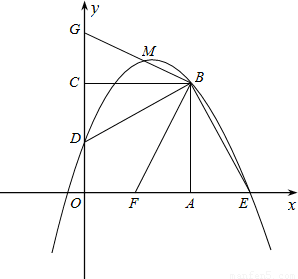
在平面直角坐標xOy中,(如圖)正方形OABC的邊長為4,邊OA在x軸的正半軸上,邊OC在y軸的正半軸上,點D是OC的中點,BE⊥DB交x軸于點E.
⑴求經過點D、B、E的拋物線的解析式;
⑵將∠DBE繞點B旋轉一定的角度后,邊BE交線段OA于點F,邊BD交y軸于點G,交⑴中的拋
物線于M(不與點B重合),如果點M的橫坐標為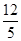 ,那么結論OF=
,那么結論OF=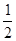 DG能成立嗎?請說明理由.
DG能成立嗎?請說明理由.
⑶過⑵中的點F的直線交射線CB于點P,交⑴中的拋物線在第一象限的部分于點Q,且使△PFE為等腰三角形,求Q點的坐標.
解:(1)∵BE⊥DB交x軸于點E,OABC是正方形,∴∠DBC=EBA。
在△BCD與△BAE中,∵∠BCD=∠BAE=90°, BC=BA ,∠DBC=∠EBA ,
∴△BCD≌△BAE(ASA)。∴AE=CD。
∵OABC是正方形,OA=4,D是OC的中點,
∴A(4,0),B(4,4),C(0,4),D(0,2),∴E(6,0).
設過點D(0,2),B(4,4),E(6,0)的拋物線解析式為y=ax2+bx+c,則有:
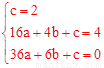 ,解得
,解得 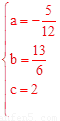 。
。
∴經過點D、B、E的拋物線的解析式為: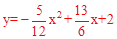 。
。
(2)結論OF= DG能成立.理由如下:
DG能成立.理由如下:
由題意,當∠DBE繞點B旋轉一定的角度后,同理可證得△BCG≌△BAF,∴AF=CG。
∵xM= ,∴
,∴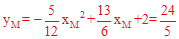 。∴M(
。∴M(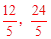 )。
)。
設直線MB的解析式為yMB=kx+b,
∵M(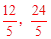 ),B(4,4),
),B(4,4),
∴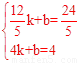 ,解得
,解得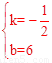 。
。
∴yMB=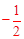 x+6。∴G(0,6)。
x+6。∴G(0,6)。
∴CG=2,DG=4。∴AF=CG=2,OF=OA﹣AF=2,F(2,0)。
∵OF=2,DG=4,∴結論OF=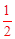 DG成立。
DG成立。
(3)如圖,△PFE為等腰三角形,可能有三種情況,分類討論如下:
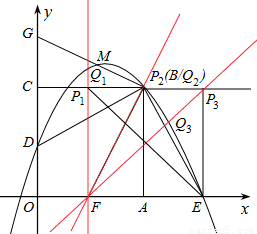
①若PF=FE。
∵FE=4,BC與OA平行線之間距離為4,
∴此時P點位于射線CB上。
∵F(2,0),∴P(2,4)。
此時直線FP⊥x軸。來]∴xQ=2。
∴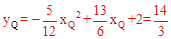 ,
,
∴Q1(2,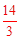 )。
)。
②若PF=PE。
如圖所示,∵AF=AE=2,BA⊥FE,∴△BEF為等腰三角形。
∴此時點P、Q與點B重合。∴Q2(4,4)。
③若PE=EF。
∵FE=4,BC與OA平行線之間距離為4,∴此時P點位于射線CB上。
∵E(6,0),∴P(6,4)。
設直線yPF的解析式為yPF=kx+b,∵F(2,0),P(6,4),
∴ ,解得
,解得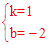 。∴yPF=x﹣2。
。∴yPF=x﹣2。
∵Q點既在直線PF上,也在拋物線上,
∴ ,化簡得5x2﹣14x﹣48=0,
,化簡得5x2﹣14x﹣48=0,
解得x1=
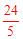 ,x2=﹣2(不合題意,舍去)。∴xQ=2。
,x2=﹣2(不合題意,舍去)。∴xQ=2。
∴yQ=xQ﹣2=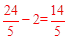 。∴Q3(
。∴Q3(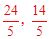 )。
)。
綜上所述,Q點的坐標為Q1(2,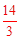 )或Q2(4,4)或Q3(
)或Q2(4,4)或Q3(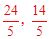 )。
)。
【解析】(1)由正方形的性質和△BCD≌△BAE求得E點坐標,然后利用待定系數法求拋物線解析式。
(2)求出M點坐標,然后利用待定系數法求直線MB的解析式,令x=0,求得G點坐標,從而得到線段CG、DG的長度;由△BCG≌△BAF,可得AF=CG,從而求得OF的長度.比較OF與DG的長度,它們滿足OF=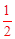 DG的關系,所以結論成立;
DG的關系,所以結論成立;
(3)分PF=FE、PF=PE和PE=EF三種情況,逐一討論并求解。


 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:
| k |
| x |
| 3 |
| x |
| k |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•渝北區一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數點(橫、縱坐標均為整數)中任意選取一個點,其橫、縱坐標之和為0的概率是
(2012•渝北區一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數點(橫、縱坐標均為整數)中任意選取一個點,其橫、縱坐標之和為0的概率是| 5 |
| 29 |
| 5 |
| 29 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•順義區二模)如圖,在平面直角坐標xOy系,一次函數y=-2x+2的圖象與x軸相交于點B,與y軸相交于點C,與反比例函數圖象相交于點A,且AB=2BC.
(2013•順義區二模)如圖,在平面直角坐標xOy系,一次函數y=-2x+2的圖象與x軸相交于點B,與y軸相交于點C,與反比例函數圖象相交于點A,且AB=2BC.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=
如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 12 |
| 5 |
| 1 |
| 2 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com