
【題目】如圖,AB為⊙O的直徑,BF切⊙O于點B,AF交⊙O于點D,點C在DF上,BC交⊙O于點E,且∠BAF=2∠CBF,CG⊥BF于點G,連接AE. 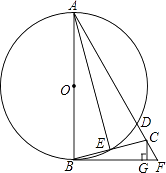
(1)直接寫出AE與BC的位置關系;
(2)求證:△BCG∽△ACE;
(3)若∠F=60°,GF=1,求⊙O的半徑長.
【答案】
(1)解:如圖1,
∵AB是⊙O的直徑,
∴∠AEB=90°.
∴AE⊥BC
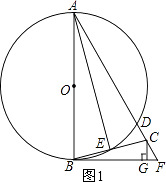
(2)解:如圖1,

∵BF與⊙O相切,
∴∠ABF=90°.
∴∠CBF=90°﹣∠ABE=∠BAE.
∵∠BAF=2∠CBF.
∴∠BAF=2∠BAE.
∴∠BAE=∠CAE.
∴∠CBF=∠CAE.
∵CG⊥BF,AE⊥BC,
∴∠CGB=∠AEC=90°.
∵∠CBF=∠CAE,∠CGB=∠AEC,
∴△BCG∽△ACE
(3)解:連接BD,如圖2所示.
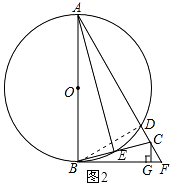
∵∠DAE=∠DBE,∠DAE=∠CBF,
∴∠DBE=∠CBF.
∵AB是⊙O的直徑,
∴∠ADB=90°.
∴BD⊥AF.
∵∠DBC=∠CBF,BD⊥AF,CG⊥BF,
∴CD=CG.
∵∠F=60°,GF=1,∠CGF=90°,
∴tan∠F= ![]() =CG=tan60°=
=CG=tan60°= ![]()
∵CG= ![]() ,
,
∴CD= ![]() .
.
∵∠AFB=60°,∠ABF=90°,
∴∠BAF=30°.
∵∠ADB=90°,∠BAF=30°,
∴AB=2BD.
∵∠BAE=∠CAE,∠AEB=∠AEC,
∴∠ABE=∠ACE.
∴AB=AC.
設⊙O的半徑為r,則AC=AB=2r,BD=r.
∵∠ADB=90°,
∴AD= ![]() r.
r.
∴DC=AC﹣AD=2r﹣ ![]() r=(2﹣
r=(2﹣ ![]() )r=
)r= ![]() .
.
∴r=2 ![]() +3.
+3.
∴⊙O的半徑長為2 ![]() +3.
+3.
【解析】(1)由AB為⊙O的直徑即可得到AE與BC垂直.(2)易證∠CBF=∠BAE,再結合條件∠BAF=2∠CBF就可證到∠CBF=∠CAE,易證∠CGB=∠AEC,從而證到△BCG∽△ACE.(3)由∠F=60°,GF=1可求出CG= ![]() ;連接BD,容易證到∠DBC=∠CBF,根據角平分線的性質可得DC=CG=
;連接BD,容易證到∠DBC=∠CBF,根據角平分線的性質可得DC=CG= ![]() ;設圓O的半徑為r,易證AC=AB,∠BAD=30°,從而得到AC=2r,AD=
;設圓O的半徑為r,易證AC=AB,∠BAD=30°,從而得到AC=2r,AD= ![]() r,由DC=AC﹣AD=
r,由DC=AC﹣AD= ![]() 可求出⊙O的半徑長.
可求出⊙O的半徑長.
【考點精析】利用角平分線的性質定理和等腰三角形的判定對題目進行判斷即可得到答案,需要熟知定理1:在角的平分線上的點到這個角的兩邊的距離相等; 定理2:一個角的兩邊的距離相等的點,在這個角的平分線上;如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(簡稱:等角對等邊).這個判定定理常用于證明同一個三角形中的邊相等.


 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:初中數學 來源: 題型:
【題目】某學校準備開展“陽光體育活動”,決定開設以下體育活動項目:足球、乒乓球、籃球和羽毛球,要求每位學生必須且只能選擇一項,為了解選擇各種體育活動項目的學生人數,隨機抽取了部分學生進行調查,并將通過調查獲得的數據進行整理,繪制出以下兩幅不完整的統計圖,請根據統計圖回答問題: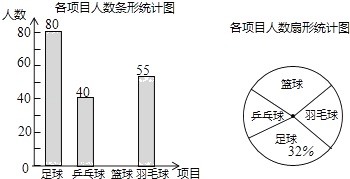
(1)這次活動一共調查了名學生;
(2)補全條形統計圖;
(3)在扇形統計圖中,選擇籃球項目的人數所在扇形的圓心角等于度;
(4)若該學校有1500人,請你估計該學校選擇足球項目的學生人數約是人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是四邊形ABCD外接圓上任意一點,且不與四邊形頂點重合,若AD是⊙O的直徑,AB=BC=CD.連接PA,PB,PC,若PA=a,則點A到PB和PC的距離之和AE+AF= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,BF切⊙O于點B,AF交⊙O于點D,點C在DF上,BC交⊙O于點E,且∠BAF=2∠CBF,CG⊥BF于點G,連接AE. 
(1)直接寫出AE與BC的位置關系;
(2)求證:△BCG∽△ACE;
(3)若∠F=60°,GF=1,求⊙O的半徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在矩形ABCD中,AB=10 cm,BC=8 cm.點P從點A出發,沿A→B→C→D的路線運動,到點D停止;點Q從點D出發,沿D→C→B→A的路線運動,到點A停止.若點P、點Q同時出發,點P的速度為每秒1 cm,點Q的速度為每秒2 cm,a秒時,點P、點Q同時改變速度,點P的速度變為每秒b cm,點Q的速度變為每秒d cm.圖②是點P出發x秒后△APD的面積S1(cm2)與時間x(秒)的函數關系圖象;圖③是點Q出發x秒后△AQD的面積S2(cm2)與時間x(秒)的函數關系圖象.
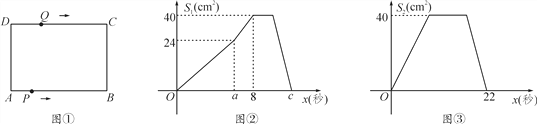
(1)參照圖②,求a、 b及圖②中c的值;
(2)求d的值;
(3)設點P離開點A的路程為y1(cm),點Q到點A還需要走的路程為y2(cm),請分別寫出改變速度后,y1、y2與出發后的運動時間x(秒)的函數關系式,并求出點P、點Q相遇時x的值;
(4)當點Q出發__ __秒時,點Q的運動路程為25 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
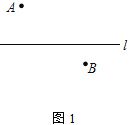
【題目】(1) 如圖1,在一條筆直的公路兩側,分別有A、B兩個村莊,現在要在公路l旁建一座火力發電廠,向A、B兩個村莊供電,為使所用的電線最短,請問供電廠P應健在何處?畫出圖形,不寫作法,保留作圖痕跡;
(2) 如圖2,若要向4個村莊A、B、C、D供電,供電廠P又該建在何處能使所用電線最短呢?畫出圖形,不寫作法,保留作圖痕跡;
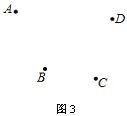
(3)A、B、C、D如圖3,連接AC并延長到E,使CE=AC,連接BD并反向延長到F,不寫作法,保留作圖痕跡.
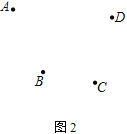
查看答案和解析>>
科目:初中數學 來源: 題型:
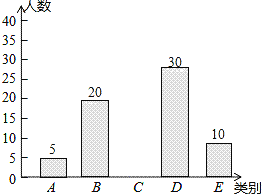
【題目】亞健康是時下社會熱門話題,進行體育鍛煉是遠離亞健康的一種重要方式,為了解某校八年級學生每天進行體育鍛煉的時間情況,隨機抽樣調查了100名初中學生,根據調查結果得到如圖所示的統計圖表.
類別 | 時間t(小時) | 人數 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
請根據圖表信息解答下列問題:
(1)a= ;
(2)補全條形統計圖;
(3)小王說:“我每天的鍛煉時間是調查所得數據的中位數”,問小王每天進行體育鍛煉的時間在什么范圍內?
(4)若把每天進行體育鍛煉的時間在1小時以上定為鍛煉達標,則被抽查學生的達標率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,將Rt△AOB繞點O順時針旋轉90°后得Rt△FOE,將線段EF繞點E逆時針旋轉90°后得線段ED,分別以O,E為圓心,OA、ED長為半徑畫弧AF和弧DF,連接AD,則圖中陰影部分面積是( ) 
A.π
B.π+5
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com