【題目】如圖①，在矩形ABCD中，AB＝10 cm，BC＝8 cm.點P從點A出發，沿A→B→C→D的路線運動，到點D停止；點Q從點D出發，沿D→C→B→A的路線運動，到點A停止．若點P、點Q同時出發，點P的速度為每秒1 cm，點Q的速度為每秒2 cm，a秒時，點P、點Q同時改變速度，點P的速度變為每秒b cm，點Q的速度變為每秒d cm.圖②是點P出發x秒后△APD的面積S1(cm2)與時間x(秒)的函數關系圖象；圖③是點Q出發x秒后△AQD的面積S2(cm2)與時間x(秒)的函數關系圖象．
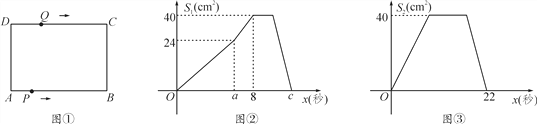
(1)參照圖②，求a、 b及圖②中c的值；
(2)求d的值；
(3)設點P離開點A的路程為y1(cm)，點Q到點A還需要走的路程為y2(cm)，請分別寫出改變速度后，y1、y2與出發后的運動時間x(秒)的函數關系式，并求出點P、點Q相遇時x的值；
(4)當點Q出發__ __秒時，點Q的運動路程為25 cm.
【答案】（1）6；2；17；（2）1；（3）
；（4）1或19.
【解析】分析：（1）根據題意和S△APD求出a，b，c的值；（2）由圖象和題易求出d的關系式，從而解出d；（3）首先求出y1，y2關于x的等量關系，然后根據題意可得y1=y2求出x的值；（4）當點Q出發17秒時，點P到達點D停止運動，點Q還需運動2秒，即共運動19秒時，可使P、Q這兩點在運動路線上相距的路程為25cm．
本題解析：
解：(1)觀察圖②，得當x＝a時，S△APD＝
PA·AD＝a×8＝24，
∴a＝6，b＝
＝2，c＝8＋
＝17.
(2)依題意，得(22－6)d＝28－12，解得d＝1.
(3)y1＝2x－6，y2＝22－x.當點P、點Q相遇時，2x－6＝22－x，得x＝
.
（4）當點Q出發17秒時，點P到達點D停止運動，點Q還需運動2秒，
即共運動19秒時，可使P、Q這兩點在運動路線上相距的路程為25cm．
點Q出發1s，則點P，Q相距25cm，設點Q出發x秒，點P、點Q相距25cm，則2x+x=28-25，解得x=1．
∴當點Q出發1或19秒時，點P、點Q在運動路線上相距的路程為25cm．
故答案為：1或19．
科目：初中數學 來源： 題型：
【題目】我們可以將任意三位數表示為
（其中a、b、c 分別表示百位上的數字，十位上的數字和個位上的數字，且a
0）顯然，= 100a+10b+c；我們把形如
和
的兩個三位數稱為一對“姊妹數”（其中x、y、z是三個連續的自然數）如：123和321是一對“姊妹數”,789和987是一對“姊妹數”.
（1）一對“姊妹數”的和為1110，求這對“姊妹數”.
（2）如果用x表示百位數字，試說明：任意一對“姊妹數”的和能被37整除.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知，在平面直角坐標系中，A（﹣3，﹣4），B（0，﹣2）．
（1）△OAB繞O點旋轉180°得到△OA1B1，請畫出△OA1B1，并寫出A1，B1的坐標；
（2）判斷以A，B，A1，B1為頂點的四邊形的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
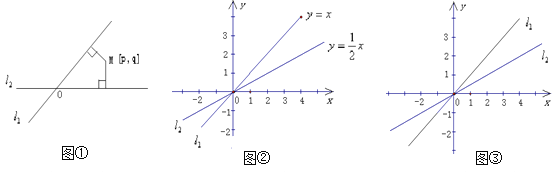
【題目】我們給出如下定義：如圖①，平面內兩條直線
、
相交于點O，對于平面內的任意一點M，若p、q分別是點M到直線和的距離（P≥0，q≥0
），稱有序非負實數對
是點M的距離坐標。
根據上述定義，請解答下列問題：
如圖②，平面直角坐標系xoy內，直線的關系式為
，直線的關系式為
，M是平面直角坐標系內的點。
（1）若
，求距離坐標為
時，點M的坐標；
（2）若
，且
，利用圖②，在第一象限內，求距離坐標為時，點M的坐標；
（3）若
，則坐標平面內距離坐標為時，點M可以有幾個位置？并用三角尺在圖③畫出符合條件的點M（簡要說明畫法）。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB為⊙O的直徑，BF切⊙O于點B，AF交⊙O于點D，點C在DF上，BC交⊙O于點E，且∠BAF=2∠CBF，CG⊥BF于點G，連接AE．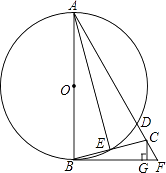 
（1）直接寫出AE與BC的位置關系；
（2）求證：△BCG∽△ACE；
（3）若∠F=60°，GF=1，求⊙O的半徑長．
查看答案和解析>>
科目：初中數學 來源： 題型：
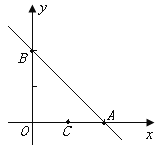
【題目】如圖，已知直線
與
軸、
軸交點分別為
、
，另一直線
經過
，且把
分成兩部分.
（1）若被分成的兩部分面積相等，求
和
的值.
（2）若被分成的兩部分面積之比為
，求和的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司到果園基地購買某種優質水果，慰問醫務工作者，果園基地對購買量在3000千克以上（含3000千克）的有兩種銷售方案，甲方案：每千克9元，由基地送貨上門．乙方案：每千克8元，由顧客自己租車運回，已知該公司租車從基地到公司的運輸費為5000元．
(1)分別寫出該公司兩種購買方案的付款y（元）與所購買的水果質量x（千克）之間的函數關系式，并寫出自變量x的取值范圍．
(2)依據購買量判斷，選擇哪種購買方案付款最少？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
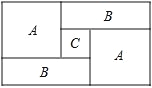
【題目】如圖，一個長方形運動場被分割成 A、B、A、B、C 共 5 個區域，A 區域是邊長為 a 米的正方形，C 區是邊長為 c 米的正方形
（1）列式表示一個 B 區長方形場地的周長，并將式子化簡；
（2）列式表示整個長方形運動場的周長，并將式子化簡；
（3）當a=4,c=2時，求運動場地的周長和面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場投入13 800元資金購進甲、乙兩種礦泉水共500箱，礦泉水的成本價和銷售價如表所示：
類別/單價 | 成本價 | 銷售價(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)該商場購進甲、乙兩種礦泉水各多少箱？
(2)全部售完500箱礦泉水，該商場共獲得利潤多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com