
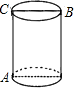
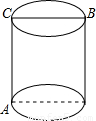
 如圖,地上有一圓柱,在圓柱下底面的A點處有一螞蟻,它想沿圓柱表面爬行.吃到上底面上與A點相對的B點處的食物(π的近似值取3,以下同).
如圖,地上有一圓柱,在圓柱下底面的A點處有一螞蟻,它想沿圓柱表面爬行.吃到上底面上與A點相對的B點處的食物(π的近似值取3,以下同).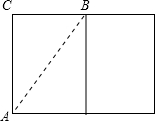 解:將圓柱體展開,連接AB,
解:將圓柱體展開,連接AB, ×2π×3=3π≈9厘米,
×2π×3=3π≈9厘米, =
= =15厘米.
=15厘米. =3π≈9,
=3π≈9,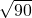 =3
=3 .
.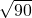 >9,
>9,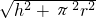 ,沿AC再經過直徑CB時,
,沿AC再經過直徑CB時,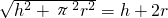 .
.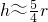 時,兩種爬行路程一樣.
時,兩種爬行路程一樣.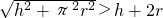 ,整理,得4h<(π2-4)r
,整理,得4h<(π2-4)r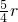 ,所以當h<
,所以當h<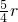 時,沿AC再經過直徑CB到點B時所走路程最短.
時,沿AC再經過直徑CB到點B時所走路程最短.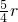 時,沿側面AB走路程最短.
時,沿側面AB走路程最短. r時,沿AC到CB走路程最短為h+2r.
r時,沿AC到CB走路程最短為h+2r. r時,沿側面AB走或沿AC到CB走路程一樣長為
r時,沿側面AB走或沿AC到CB走路程一樣長為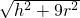 或h+2r.
或h+2r. r時,沿側面AB走路程最短為
r時,沿側面AB走路程最短為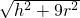 .
. r時,沿AC到CB走路程最短為h+2r.
r時,沿AC到CB走路程最短為h+2r.

 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:初中數學 來源: 題型:
 如圖,地上有一圓柱,在圓柱下底面的A點處有一螞蟻,它想沿圓柱表面爬行,吃到上底面與A點相對的B點處的食物,當圓柱的高h=12π厘米,底面半徑r=9厘米時,螞蟻沿側面爬行的最短路程是
如圖,地上有一圓柱,在圓柱下底面的A點處有一螞蟻,它想沿圓柱表面爬行,吃到上底面與A點相對的B點處的食物,當圓柱的高h=12π厘米,底面半徑r=9厘米時,螞蟻沿側面爬行的最短路程是查看答案和解析>>
科目:初中數學 來源: 題型:
 (2007•西城區二模)如圖,地上有一圓柱,在圓柱下底面的A點處有一螞蟻,它想沿圓柱表面爬行.吃到上底面上與A點相對的B點處的食物(π的近似值取3,以下同).
(2007•西城區二模)如圖,地上有一圓柱,在圓柱下底面的A點處有一螞蟻,它想沿圓柱表面爬行.吃到上底面上與A點相對的B點處的食物(π的近似值取3,以下同).查看答案和解析>>
科目:初中數學 來源:2010-2011學年北京市北大附中九年級(上)期末數學試卷(解析版) 題型:填空題
查看答案和解析>>
科目:初中數學 來源:2007年北京市西城區中考數學二模試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com