解:(1)如圖:
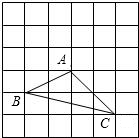
S
△ABC=2a×4a-

a×2a-

×2a×2a-

a×4a=3a
2;
(2)構造△ABC所示,(未在試卷上畫出圖形不扣分)
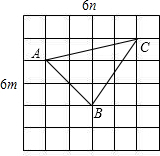
S
△ABC=3m×4n-

×m×4n-

×3m×2n-

×2m×2n=5mn.
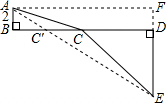
(3)如圖所示:已知AB=2,DE=5,BD=3,
AB⊥BD,DE⊥BD,當AE在一條直線上時,AC+CE最小,
由題意得出:AB∥DE,
∴△ABC′∽△EDC′,
∴
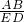
=
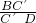
,
∴

=
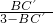
,
解得:BC′=

,C′D=3-

=

,
過點A作AF∥BD,交DE的延長線于F點,
根據題意,四邊形ABDF為矩形.
EF=AB+DE=2+5=7,AF=DB=3.
∴AE=
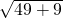
=

.
即AC+CE的最小值是

,
故:a=

,b=3-

=

時,

+
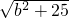
有最小值為

.
(4)證明:∵a
2+b
2=c
2,c
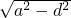
=a
2,
∴c
2(a
2-d
2)=a
4,
則(a
2+b
2)(a
2-d
2)=a
4,
整理得出:a
2b
2=a
2d
2+b
2d
2,
∴a
2b
2=d
2(a
2+b
2),
∴a
2b
2=d
2c
2,
∵a,b,c,d都是正數,
∴ab=cd.
分析:(1)

a是直角邊長為a,2a的直角三角形的斜邊;2

a是直角邊長為2a,2a的直角三角形的斜邊;

a是直角邊長為a,4a的直角三角形的斜邊,把它整理為一個矩形的面積減去三個直角三角形的面積;
(2)結合(1)易得此三角形的三邊分別是直角邊長為m,4n的直角三角形的斜邊;直角邊長為3m,2n的直角三角形的斜邊;直角邊長為2m,2n的直角三角形的斜邊.同樣把它整理為一個矩形的面積由(1)的結果可作BD=12,過點A作AF∥BD,交DE的延長線于F點,使AB=2,ED=3,連接AE交BD于點C,然后構造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性質(3)可作BD=3,過點A作AF∥BD,交DE的延長線于F點,使AB=2,ED=5,連接AE交BD于點C,然后構造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性質可求得AE的值就是代數式

+
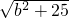
的最小值.
(4)根據a
2+b
2=c
2,c
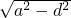
=a
2,得出c
2(a
2-d
2)=a
4,進而得出(a
2+b
2)(a
2-d
2)=a
4,再去括號得出a
2b
2=d
2c
2,即可得出答案.
點評:此題主要考查了最短路線問題以及勾股定理應用,利用了數形結合的思想,通過構造直角三角形,利用勾股定理求解是解題關鍵.,關鍵是結合網格用矩形及容易求得面積的直角三角形表示出所求三角形的面積進行解答.

 、
、 、
、 ,求這個三角形的面積.
,求這個三角形的面積.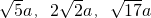 (a>0),請利用圖②的正方形網格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.
(a>0),請利用圖②的正方形網格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.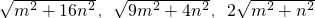 (m>0,n>0,且m≠n),試運用構圖法求出這三角形的面積.
(m>0,n>0,且m≠n),試運用構圖法求出這三角形的面積. +
+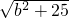 有最小值,并求這個最小值.
有最小值,并求這個最小值.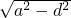 =a2,求證:ab=cd.
=a2,求證:ab=cd.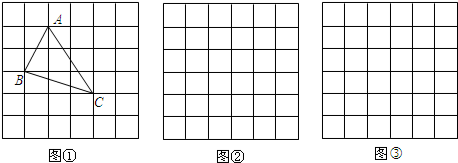

 a×2a-
a×2a- ×2a×2a-
×2a×2a- a×4a=3a2;
a×4a=3a2;
 ×m×4n-
×m×4n- ×3m×2n-
×3m×2n- ×2m×2n=5mn.
×2m×2n=5mn. 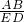 =
=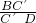 ,
, =
=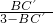 ,
, ,C′D=3-
,C′D=3- =
= ,
,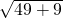 =
= .
. ,
, ,b=3-
,b=3- =
= 時,
時, +
+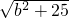 有最小值為
有最小值為 .
.
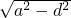 =a2,
=a2, a是直角邊長為a,2a的直角三角形的斜邊;2
a是直角邊長為a,2a的直角三角形的斜邊;2 a是直角邊長為2a,2a的直角三角形的斜邊;
a是直角邊長為2a,2a的直角三角形的斜邊; a是直角邊長為a,4a的直角三角形的斜邊,把它整理為一個矩形的面積減去三個直角三角形的面積;
a是直角邊長為a,4a的直角三角形的斜邊,把它整理為一個矩形的面積減去三個直角三角形的面積; +
+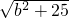 的最小值.
的最小值.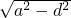 =a2,得出c2(a2-d2)=a4,進而得出(a2+b2)(a2-d2)=a4,再去括號得出a2b2=d2c2,即可得出答案.
=a2,得出c2(a2-d2)=a4,進而得出(a2+b2)(a2-d2)=a4,再去括號得出a2b2=d2c2,即可得出答案.

 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案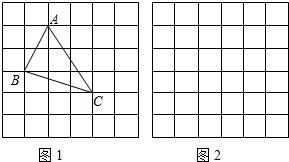
 點都在小正方形的頂點處),如圖1所示.這樣不需求△ABC的高,而借用網格就能計算出它的面積.
點都在小正方形的頂點處),如圖1所示.這樣不需求△ABC的高,而借用網格就能計算出它的面積.
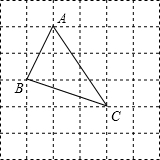 問題背景:“在△ABC中,AB、BC、AC三邊的長分別為
問題背景:“在△ABC中,AB、BC、AC三邊的長分別為 問題背景:在△ABC中,AB、BC、AC三邊的長分別為
問題背景:在△ABC中,AB、BC、AC三邊的長分別為