Question

一個正多邊形的每個外角都是72°，則這個正多邊形的對角線有（ ）條．
A．3
B．4
C．5
D．6

Answer 1

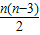
【答案】分析：因為是正多邊形，所以每個外角都相等，根據多邊形的外角和是360°，很容易確定邊數．正多邊形的邊數確定了，那么根據一個多邊形有條對角線，很容易算出有多少條．
解答：解：∵每個外角都是72°，
∴這個多邊形的邊數為：360°÷72°=5，
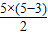
∴==5（條），
∴這個正多邊形的對角線是5條．
故選C．
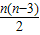
點評：本題主要考查的是多邊的外角和，多邊形的對角線及正多邊形的概念和性質，任意多邊形的外角和都是360°，和邊數無關．正多邊形的每個外角都相等．任何多邊形的對角線條數為條．