已知Rt△ABC和Rt△ADC有公共斜邊AC,M、N分別是AC、BD的中點(diǎn),且M、N不重合,請(qǐng)你畫(huà)出圖形后回答,線段MN與BD是否垂直?并請(qǐng)說(shuō)明理由.若∠BAC=30°,∠CAD=45°,AC=8cm,求MN的長(zhǎng).
分析:根據(jù)題意畫(huà)出圖形后可知本題有兩種情況,即B、D在線段AC的同側(cè)和B、D在線段AC的異側(cè).
解答:解:如圖一:連接BM、MD,延長(zhǎng)DM,過(guò)B作DM延長(zhǎng)線的垂線段BE,
則可知在Rt△BEM中∠EMB=30°,
∵AC=8,∴BM=4,
∴BE=2,EM=2
,MD=4,
從而可知BD=
=4,
∴MN=
=(-)cm,
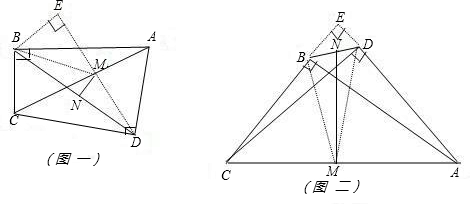
如圖二:連接BM、MD,延長(zhǎng)AD,過(guò)B作垂線段BE,在Rt△BED中,可知∠EDB=60°,
令ED=x,則BE=
x,AD=4
,AB=4
,
∴可得:
(4)2=(x)2+(x+4)2,
解得
x=-,
∴MN=
=(
+
)cm.
點(diǎn)評(píng):本題考查了勾股定理的應(yīng)用及直角三角形的相關(guān)知識(shí),解決此題很容易漏掉另外一種情況.




 名校課堂系列答案
名校課堂系列答案
 相切,D為切點(diǎn),AD∥BC.
相切,D為切點(diǎn),AD∥BC.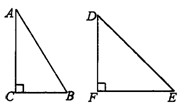 14、如圖,已知Rt△ABC和Rt△DEF不相似,其中∠C,∠F為直角,∠A<∠D,能否分別將兩個(gè)三角形分割成兩個(gè)三角形,使△ABC所分的兩個(gè)三角形與△DEF所分的兩個(gè)三角形分別相似?如果能夠,請(qǐng)?jiān)O(shè)計(jì)一個(gè)分割方案;如果不能,請(qǐng)說(shuō)明理由.
14、如圖,已知Rt△ABC和Rt△DEF不相似,其中∠C,∠F為直角,∠A<∠D,能否分別將兩個(gè)三角形分割成兩個(gè)三角形,使△ABC所分的兩個(gè)三角形與△DEF所分的兩個(gè)三角形分別相似?如果能夠,請(qǐng)?jiān)O(shè)計(jì)一個(gè)分割方案;如果不能,請(qǐng)說(shuō)明理由.
 如圖,已知Rt△ABC和三角形外一點(diǎn)P,按要求完成圖形:
如圖,已知Rt△ABC和三角形外一點(diǎn)P,按要求完成圖形: