
【題目】如圖,![]() 和
和![]() 都是等邊三角形,點
都是等邊三角形,點![]() 在
在![]() 的延長線上.
的延長線上.

(1)找出圖中一對全等三角形,并證明其全等;
(2)求![]() 的度數?若
的度數?若![]() ,
,![]() ,求
,求![]() 的長。
的長。
【答案】(1)△ABD≌△ACE,證明見解析;(2)60°,5
【解析】
(1)根據等邊三角形的性質推出AB=AC,AD=AE,∠BAC=∠DAE=60°,根據SAS可證△ABD≌△ACE;
(2)根據全等三角形的性質推出∠ABD=∠ACE,根據∠BAC+∠ABD=∠ACE+∠BEC,推出∠BEC=∠BAC=60°即可.
(1)△ABD≌△ACE,證明如下,
∵△ABC和△ADE是等邊三角形,
∴AB=AC,AD=AE, ∠BAC=∠DAE,
∴∠BAD=∠CAE,
∴△ABD≌△ACE.
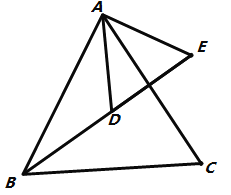
(2)如圖,設AC與BE交于點O,
∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AOB=∠EOC, ∠AOB+∠ABE+∠BAC=∠EOC+∠ACE+∠BEC,
∴∠BEC=∠BAC=60°,
即∠BEC =60°;
∵△ABD≌△ACE,
∴BD=CE=3,
∵△ADE是等邊三角形,
∴DE=AE=2,
∴BE=BD+DE=3+2=5


科目:初中數學 來源: 題型:
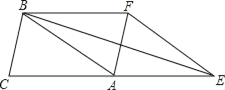
【題目】如圖,已知△ABC的面積為3,且AB=AC,現將△ABC沿CA方向平移CA長度得到△EFA.
(1)求四邊形CEFB的面積;
(2)試判斷AF與BE的位置關系,并說明理由;
(3)若∠BEC=15°,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:一個自然數,右邊的數字總比左邊的數字小,我們稱它為“下滑數”(如:32,641,8531等).現從兩位數中任取一個,恰好是“下滑數”的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在正方形ABCD中,M是BC邊(不含端點B、C)上任意一點,P是BC延長線上一點,N是![]() 的平分線上一點,若
的平分線上一點,若![]() ,求證:
,求證:![]() 為等腰三角形.下面給出此問題一種證明的思路,你可以按這一思路繼續完成證明,也可以選擇另外的方法證明此結論.證明:在AB邊上截取AE=MC,連接ME,在正方形ABCD中,
為等腰三角形.下面給出此問題一種證明的思路,你可以按這一思路繼續完成證明,也可以選擇另外的方法證明此結論.證明:在AB邊上截取AE=MC,連接ME,在正方形ABCD中,![]() ,AB=BC,
,AB=BC,![]() (下面請你連接AN,完成余下的證明過程)
(下面請你連接AN,完成余下的證明過程)
(2)若將(1)中的“正方形ABCD”改為“正三角形ABC”(如圖2),N是![]() 的平分線上一點,則當
的平分線上一點,則當![]() 時,試探究
時,試探究![]() 是何種特殊三角形,并證明探究結論.
是何種特殊三角形,并證明探究結論.
(3)若將(1)中的“正方形ABCD”改為“正![]() 邊形
邊形![]() ,試猜想:當
,試猜想:當![]() 的大小為多少時,(1)中的結論仍然成立?
的大小為多少時,(1)中的結論仍然成立?
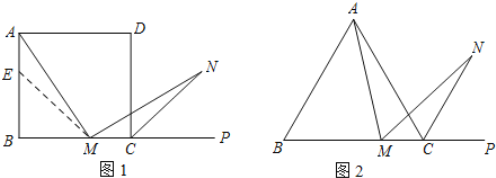
查看答案和解析>>
科目:初中數學 來源: 題型:
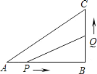
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .動點
.動點![]() ,
,![]() 分別從點
分別從點![]() ,
,![]() 同時開始移動,點
同時開始移動,點![]() 的速度為
的速度為![]() 秒,點
秒,點![]() 的速度為
的速度為![]() 秒,點
秒,點![]() 移動到點
移動到點![]() 后停止,點
后停止,點![]() 也隨之停止運動.下列時間瞬間中,能使
也隨之停止運動.下列時間瞬間中,能使![]() 的面積為
的面積為![]() 的是( )
的是( )
A. 2秒鐘 B. 3秒鐘 C. 4秒鐘 D. 5秒鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△ABC的位置如圖所示.
(1)分別寫出下列頂點的坐標:A_______,B______.
(2)頂點A關于y軸對稱的點A′的坐標為:A′_______.
(3)△ABC的面積為_______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為更好地開展“傳統文化進校園”活動,隨機抽查了部分學生,了解他們最喜愛的傳統文化項目類型(分為書法、圍棋、戲劇、國畫共4類),并將統計結果繪制成如圖不完整的頻數分布表及頻數分布直方圖.
最喜愛的傳統文化項目類型頻數分布表


根據以上信息完成下列問題:
(1)直接寫出頻數分布表中a的值;
(2)補全頻數分布直方圖;
(3)若全校共有學生1500名,估計該校最喜愛圍棋的學生大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直角△ABC中,∠C=90°,∠A=30°,AB=4,以AC為腰,在△ABC外作頂角為30°的等腰三角形ACD,連接BD.請畫出圖形,并直接寫出△BCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y1=ax2﹣![]() x+c與x軸交于點A和點B(1,0),與y軸交于點C(0,
x+c與x軸交于點A和點B(1,0),與y軸交于點C(0,![]() ),拋物線y1的頂點為G,GM⊥x軸于點M.將拋物線y1平移后得到頂點為B且對稱軸為直線l的拋物線y2.
),拋物線y1的頂點為G,GM⊥x軸于點M.將拋物線y1平移后得到頂點為B且對稱軸為直線l的拋物線y2.

(1)求拋物線y2的解析式;
(2)如圖2,在直線l上是否存在點T,使△TAC是等腰三角形?若存在,請求出所有點T的坐標;若不存在,請說明理由;
(3)點P為拋物線y1上一動點,過點P作y軸的平行線交拋物線y2于點Q,點Q關于直線l的對稱點為R,若以P,Q,R為頂點的三角形與△AMG全等,求直線PR的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com