
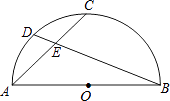
【題目】如圖,AB是半圓O的直徑,點C是 ![]() 的中點,點D是
的中點,點D是 ![]() 的中點,連接AC,BD交于點E,則
的中點,連接AC,BD交于點E,則 ![]() =( )
=( )
A.![]()
B.![]()
C.1﹣ ![]()
D.![]()
【答案】D
【解析】連接AD、CD,作AF∥CD,交BE于F,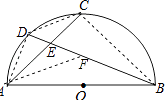
∵點D是弧AC的中點,
∴可設AD=CD=1,
根據平行線的性質得∠AFD=∠CDF=45°.
∴△ADF是等腰直角三角形,
則AF= ![]() ,BF=AF=
,BF=AF= ![]() .
.
∴BD= ![]() +1.
+1.
∵∠DAC=∠ABD,∠ADB=∠ADB,
∴△ADE∽△BDA,
∴DE= ![]() =
= ![]() ﹣1,BE=2.
﹣1,BE=2.
∴ ![]() =
= ![]() .
.
所以答案是:D.
【考點精析】根據題目的已知條件,利用圓心角、弧、弦的關系和圓周角定理的相關知識可以得到問題的答案,需要掌握在同圓或等圓中,相等的圓心角所對的弧相等,所對的弦也相等;在同圓或等圓中,同弧等弧所對的圓周角相等,都等于這條弧所對的圓心角的一半;頂點在圓心上的角叫做圓心角;頂點在圓周上,且它的兩邊分別與圓有另一個交點的角叫做圓周角;一條弧所對的圓周角等于它所對的圓心角的一半.


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,點D,E分別是邊BC,AB上的中點,連接DE并延長至點F,使EF=2DE,連接CE、AF.
(1)證明:AF=CE;
(2)當∠B=30°時,試判斷四邊形ACEF的形狀并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC為等腰直角三角形,∠ACB=90°,拋物線y=﹣x2+bx+c經過A,B兩點,其中點A,C的坐標分別為(1,0),(﹣4,0),拋物線的頂點為點D.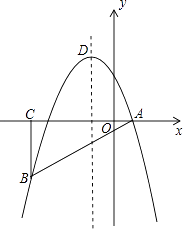
(1)求拋物線的解析式;
(2)點E是直角三角形ABC斜邊AB上的一個動點(不與A,B重合),過點E作x軸的垂線,交拋物線于點F,當線段FE的長度最大時,求點E的坐標;
(3)在(2)的條件下,拋物線上是否存在一點P,使△PEF是以EF為直角邊的直角三角形?若存在,求出所有點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代數學的經典著作,書中有一個問題:“今有黃金九枚,白銀一十一枚,稱之重適等.交易其一,金輕十三兩.問金、銀一枚各重幾何?”.意思是:今有甲種袋子中裝有黃金9枚(每枚黃金重量相同),乙種袋子中裝有白銀11枚(每枚白銀重量相同),稱重兩袋相等.兩袋互相交換1枚后,甲種袋子比乙種袋子輕了13兩(袋子重量忽略不計).問黃金、白銀每枚各重多少兩?設每枚黃金重x兩,每枚白銀重y兩,則可建立方程為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了迎接體育中考,某校九年級開展了體育中考項目的第一次模擬測驗. 下圖為某校九年級同學各項目達標人數統計圖: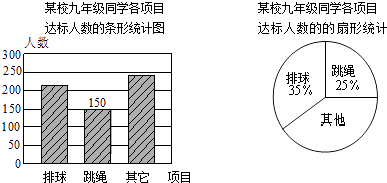
(1)在九年級學生中,達標的總人數是;
(2)在扇形統計圖中,表示“其他”項目扇形的圓心角的度數是;
(3)經過一段時間的練習,在第二次模擬測驗中,“排球”項目達標的人數增長到了231人,則“排球”項目達標人數的增長率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場準備進一批兩種不同型號的衣服,已知購進![]() 種型號衣服9件,
種型號衣服9件,![]() 種型號衣服10件,則共需1810元;若購進
種型號衣服10件,則共需1810元;若購進![]() 種型號衣服12件,
種型號衣服12件,![]() 種型號衣服8件,共需1880元;已知銷售一件
種型號衣服8件,共需1880元;已知銷售一件![]() 型號衣服可獲利18元,銷售一件
型號衣服可獲利18元,銷售一件![]() 型號衣服可獲利30元.要使在這次銷售中獲利不少于699元,且
型號衣服可獲利30元.要使在這次銷售中獲利不少于699元,且![]() 型號衣服不多于28件.
型號衣服不多于28件.
(1)求![]() 型號衣服進價各是多少元?
型號衣服進價各是多少元?
(2)若已知購進![]() 型號衣服是
型號衣服是![]() 型號衣服的2倍還多4件,則商店在這次進貨中可有幾種方案?并簡述購貨方案.
型號衣服的2倍還多4件,則商店在這次進貨中可有幾種方案?并簡述購貨方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知Rt△ABC中,∠ABC=90°,先把△ABC繞點B順時針旋轉90°至△DBE后,再把△ABC沿射線平移至△FEG,DE、FG相交于點H.

(1)判斷線段DE、FG的位置關系,并說明理由;
(2)連結CG,求證:四邊形CBEG是正方形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com