
【題目】如圖,∠ABC=90°,D、E分別在BC、AC上,AD⊥DE,且AD=DE,點F是AE的中點,FD與AB相交于點M.
(1)求證:∠FMC=∠FCM;
(2)AD與MC垂直嗎?并說明理由.

【答案】(1)證明見解析;(2)AD⊥MC,理由見解析.
【解析】試題分析:(1)根據等腰直角三角形的性質得出DF⊥AE,DF=AF=EF,進而利用全等三角形的判定得出△DFC≌△AFM(AAS),即可得出答案;
(2)由(1)知,∠MFC=90°,FD=EF,FM=FC,即可得出∠FDE=∠FMC=45°,即可理由平行線的判定得出答案.
(1)證明:∵△ADE是等腰直角三角形,F是AE中點,
∴DF⊥AE,DF=AF=EF,
又∵∠ABC=90°,
∠DCF,∠AMF都與∠MAC互余,
∴∠DCF=∠AMF,
在△DFC和△AFM中,
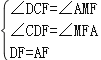 ,
,
∴△DFC≌△AFM(AAS),
∴CF=MF,
∴∠FMC=∠FCM;
(2)AD⊥MC,
理由:由(1)知,∠MFC=90°,FD=FA=FE,FM=FC,
∴∠FDE=∠FMC=45°,
∴DE∥CM,
∴AD⊥MC.


科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象與反比例函數y= ![]() 的圖象交于點A(﹣2,﹣5 ),C (5,n),交y軸于點B,交x軸于點D,那么不等式kx+b﹣
的圖象交于點A(﹣2,﹣5 ),C (5,n),交y軸于點B,交x軸于點D,那么不等式kx+b﹣ ![]() >0的解集是 .
>0的解集是 . 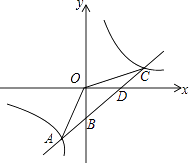
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直徑坐標系中,反比例函數y= ![]() (x>0)的圖象上有一點A(m,4),過點A作AB⊥x軸于點B,將點B向右平移2個單位長度得到點C,過點C作y軸的平行線交反比例函數的圖象于點D,CD=
(x>0)的圖象上有一點A(m,4),過點A作AB⊥x軸于點B,將點B向右平移2個單位長度得到點C,過點C作y軸的平行線交反比例函數的圖象于點D,CD= ![]()
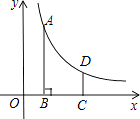
(1)點D的橫坐標為(用含m的式子表示);
(2)求反比例函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足為D,AN是△ABC外角∠CAM的平分線,CE⊥AN,垂足為E.
(1)求證:四邊形ADCE是矩形;
(2)當△ABC滿足什么條件時,四邊形ADCE是正方形?給出證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列結論:①AC﹣BE=AE;②點E在線段BC的垂直平分線上;③∠DAE=∠C;④BC=4AD,其中正確的有( )
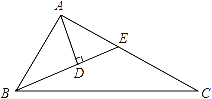
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將九年級部分男生擲實心球的成績進行整理,分成5個小組(x表示成績,單位:米).A組:5.25≤x<6.25;B組:6.25≤x<7.25;C組:7.25≤x<8.25;D組:8.25≤x<9.25;E組:9.25≤x<10.25,并繪制出扇形統計圖和頻數分布直方圖(不完整).規定x≥6.25為合格,x≥9.25為優秀.
(1)這部分男生有多少人?其中成績合格的有多少人?
(2)這部分男生成績的中位數落在哪一組?扇形統計圖中D組對應的圓心角是多少度?
(3)要從成績優秀的學生中,隨機選出2人介紹經驗,已知甲、乙兩位同學的成績均為優秀,求他倆至少有1人被選中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織了一次G20知識競賽活動,根據獲獎同學在競賽中的成績制成的統計圖表如下,仔細閱讀圖表解答問題: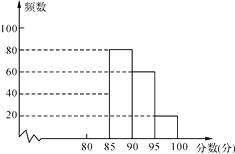
分數段 | 頻數 | 頻率 |
80≤x<85 | a | 0.2 |
85≤x<90 | 80 | b |
90≤x<95 | 60 | c |
95≤x<100 | 20 | 0.1 |
(1)求出表中a,b,c的數值,并補全頻數分布直方圖;
(2)獲獎成績的中位數落在哪個分數段?
(3)估算全體獲獎同學成績的平均分.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下面一列數,探求其規律:
![]() ,-
,-![]() ,
,![]() ,-
,-![]() ,
,![]() ,-
,-![]() ,…
,…
(1) 寫出第7,8,9項的三個數;
(2) 第2 018個數是什么?
(3) 如果這一列數無限排列下去,與 ____ 、____ 兩數越來越接近?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com