
【題目】如圖,已知拋物線與x軸交于A(﹣1,0)、E(3,0)兩點,與y軸交于點B(0,3).
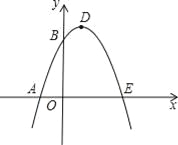
(1)求拋物線的解析式;
(2)設拋物線頂點為D,求四邊形AEDB的面積;
(3)△AOB與△DBE是否相似?如果相似,請給以證明;如果不相似,請說明理由.
【答案】(1)![]() ;(2)9;(3)△AOB∽△DBE.理由見解析.
;(2)9;(3)△AOB∽△DBE.理由見解析.
【解析】
(1)易得c=3,故設拋物線解析式為y=ax2+bx+3,根據拋物線所過的三點的坐標,可得方程組,解可得a、b的值,即可得解析式;
(2)易由頂點坐標公式得頂點坐標,根據圖形間的關系可得四邊形ABDE的面積=![]() ,代入數值可得答案;
,代入數值可得答案;
(3)根據題意,易得∠AOB=∠DBE=90°,且![]() ,即可判斷出兩三角形相似.
,即可判斷出兩三角形相似.
(1)∵拋物線與y軸交于點(0,3),
∴設拋物線解析式為y=ax2+bx+3(a≠0)
根據題意,得![]() ,
,
解得![]() .
.
∴拋物線的解析式為y=﹣x2+2x+3;
(2)如圖,設該拋物線對稱軸是DF,連接DE、BD.過點B作BG⊥DF于點G.
由頂點坐標公式得頂點坐標為D(1,4)
設對稱軸與x軸的交點為F
∴四邊形ABDE的面積=![]()
=![]() AOBO+
AOBO+![]() (BO+DF)OF+
(BO+DF)OF+![]() EFDF
EFDF
=![]() ×1×3+
×1×3+![]() ×(3+4)×1+
×(3+4)×1+![]() ×2×4
×2×4
=9;
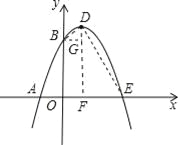
(3)相似,如圖,
BD=![]() ;
;
∴BE=![]()
DE=![]() =
=![]()
∴BD2+BE2=20,DE2=20
即:BD2+BE2=DE2,
所以△BDE是直角三角形
∴∠AOB=∠DBE=90°,且![]() ,
,
∴△AOB∽△DBE.



 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:初中數學 來源: 題型:
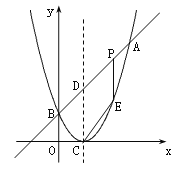
【題目】如圖,已知二次函數圖象的頂點坐標為C(1,0),直線![]() 與該二次函數的圖象交于A、B兩點,其中A點的坐標為(3,4),B點在軸
與該二次函數的圖象交于A、B兩點,其中A點的坐標為(3,4),B點在軸![]() 上.
上.
(1)求![]() 的值及這個二次函數的關系式;
的值及這個二次函數的關系式;
(2)P為線段AB上的一個動點(點P與A、B不重合),過P作![]() 軸的垂線與這個二次函數的圖象交于點E點,設線段PE的長為
軸的垂線與這個二次函數的圖象交于點E點,設線段PE的長為![]() ,點P的橫坐標為
,點P的橫坐標為![]() ,求
,求![]() 與
與![]() 之間的函數關系式,并寫出自變量
之間的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(3)D為直線AB與這個二次函數圖象對稱軸的交點,在線段AB上是否存在一點P,使得四邊形DCEP是平行四邊形?若存在,請求出此時P點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 的解析式為
的解析式為![]() ,(與
,(與![]() 軸交于點
軸交于點![]() (點
(點![]() 在點
在點![]() 左側),與
左側),與![]() 軸交于點
軸交于點![]() ,項點為
,項點為![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)若將拋物線![]() 沿著直線
沿著直線![]() 的方向平移得到拋物線
的方向平移得到拋物線![]() ;
;
①當拋物線![]() 與直線
與直線![]() 只有一個公共點時,求拋物線
只有一個公共點時,求拋物線![]() 的解析式;
的解析式;
②點![]() 是①中拋物線上一點,若
是①中拋物線上一點,若![]() 且
且![]() 為整數,求滿足條件的點
為整數,求滿足條件的點![]() 的個數.
的個數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應垃圾分類處理,改善生態環境的號召,某小區將生活垃圾分成四類:廚余垃圾、可回收垃圾、不可回收垃圾、有害垃圾,分別記為a、b、c、![]() 并且設置了相應的垃圾箱:“廚余垃圾”箱,“可回收垃圾”箱,“不可回收垃圾”箱,“有害垃圾”箱,分別記為A,B,C,D.
并且設置了相應的垃圾箱:“廚余垃圾”箱,“可回收垃圾”箱,“不可回收垃圾”箱,“有害垃圾”箱,分別記為A,B,C,D.
![]() 如果將一袋有害垃圾任意投放進垃圾箱,則投放正確的概率是________.
如果將一袋有害垃圾任意投放進垃圾箱,則投放正確的概率是________.
![]() 小明將家里的廚余垃圾、可回收垃圾分裝在兩個袋中,任意投放在其中兩個垃圾箱中,用畫樹狀圖或列表的方法求這兩袋垃圾都投放正確的概率.
小明將家里的廚余垃圾、可回收垃圾分裝在兩個袋中,任意投放在其中兩個垃圾箱中,用畫樹狀圖或列表的方法求這兩袋垃圾都投放正確的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學藝術節期間,向學校學生征集書畫作品.九年級美術李老師從全年級14個班中隨機抽取了A、B、C、D四個班,對征集到的作品的數量進行了分析統計,制作了如下兩幅不完整的統計圖.
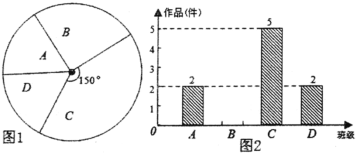
(1)李老師采取的調查方式是______________(填“普查”或“抽樣調查”),李老師所調查的4個班征集到作品共_________件,其中B班征集到作品_______________件.
(2)如果全年級參展作品中有4件獲得一等獎,其中有2名作者是男生,2名作者是女生.現在要抽取兩人去參加學校總結表彰座談會,求恰好抽中一男一女的概率.(要求用樹狀圖或列表法寫出分析過程).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,l是經過A(2,0),B(0,b)兩點的直線,且b0,點C的坐標為(2,0),當點B移動時,過點C作CD⊥l交于點D.
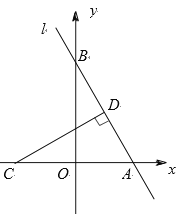
(1)求點D,O之間的距離;
(2)當tan∠CDO=![]() 時,求直線l的解析式;
時,求直線l的解析式;
(3)在(2)的條件下,直接寫出△ACD與△AOB重疊部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展以“學習朱子文化,弘揚理學思想”為主題的讀書月活動,并向學生征集讀后感,學校將收到的讀后感篇數按年級進行統計,繪制了以下兩幅統計圖(不完整).
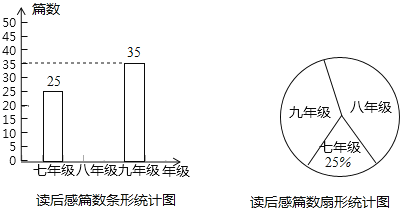
據圖中提供的信息完成以下問題
(1)扇形統計圖中“八年級”對應的圓心角是 °,并補全條形統計圖;
(2)經過評審,全校有4篇讀后感榮獲特等獎,其中有一篇來自七年級,學校準備從特等獎讀后感中任選兩篇在校廣播電臺上播出,請利用畫樹狀圖或列表的方法求出七年級特等獎讀后感被校廣播電臺播出的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為倡導節能環保,降低能源消耗,提倡環保型新能源開發,造福社會.某公司研發生產一種新型智能環保節能燈,成本為每件40元.市場調查發現,該智能環保節能燈每件售價y(元)與每天的銷售量為x(件)的關系如圖,為推廣新產品,公司要求每天的銷售量不少于1000件,每件利潤不低于5元.
(1)求每件銷售單價y(元)與每天的銷售量為x(件)的函數關系式并直接寫出自變量x的取值范圍;
(2)設該公司日銷售利潤為P元,求每天的最大銷售利潤是多少元?
(3)在試銷售過程中,受國家政策扶持,毎銷售一件該智能環保節能燈國家給予公司補貼m(m≤40)元.在獲得國家每件m元補貼后,公司的日銷售利潤隨日銷售量的增大而增大,則m的取值范圍是 (直接寫出結果).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝店老板到廠家選購![]() 、
、![]() 兩種品牌的羽絨服,
兩種品牌的羽絨服,![]() 品牌羽絨服每件進價比
品牌羽絨服每件進價比![]() 品牌羽絨服每件進價多
品牌羽絨服每件進價多![]() 元,若用
元,若用![]() 元購進
元購進![]() 種羽絨服的數量是用
種羽絨服的數量是用![]() 元購進
元購進![]() 種羽絨服數量的
種羽絨服數量的![]() 倍.
倍.
(1)求![]() 、
、![]() 兩種品牌羽絨服每件進價分別為多少元?
兩種品牌羽絨服每件進價分別為多少元?
(2)若![]() 品牌羽絨服每件售價為
品牌羽絨服每件售價為![]() 元,
元,![]() 品牌羽絨服每件售價為
品牌羽絨服每件售價為![]() 元,服裝店老板決定一次性購進
元,服裝店老板決定一次性購進![]() 、
、![]() 兩種品牌羽絨服共
兩種品牌羽絨服共![]() 件,在這批羽絨服全部出售后所獲利潤不低于
件,在這批羽絨服全部出售后所獲利潤不低于![]() 元,則最少購進
元,則最少購進![]() 品牌羽絨服多少件?
品牌羽絨服多少件?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com