
【題目】某自行車制造廠開發了一款新式自行車,計劃![]() 月份生產安裝
月份生產安裝![]() 輛,由于抽調不出足夠的熟練工來完成新式自行車的安裝,工廠決定招聘一些新工人;他們經過培訓后也能獨立進行安裝.調研部門發現:
輛,由于抽調不出足夠的熟練工來完成新式自行車的安裝,工廠決定招聘一些新工人;他們經過培訓后也能獨立進行安裝.調研部門發現: ![]() 名熟練工和
名熟練工和![]() 名新工人每日可安裝輛自行車;
名新工人每日可安裝輛自行車; ![]() 名熟練工和
名熟練工和![]() 名新工人每日可安裝
名新工人每日可安裝![]() 輛自行車。
輛自行車。
(1)每名熟練工和新工人每日分別可以安裝多少輛自行車?
(2)如果工廠招聘![]() 名新工人(
名新工人(![]() ).使得招聘的新工人和抽調熟練工剛好能完成
).使得招聘的新工人和抽調熟練工剛好能完成![]() 月份(
月份(![]() 天)的安裝任務,那么工廠有哪幾種新工人的招聘方案?
天)的安裝任務,那么工廠有哪幾種新工人的招聘方案?
(3)該自行車關于輪胎的使用有以下說明:本輪胎如安裝在前輪,安全行使路程為![]() 千公里;如安裝在后輪,安全行使路程為
千公里;如安裝在后輪,安全行使路程為![]() 千公里.請問一對輪胎能行使的最長路程是多少千公里?
千公里.請問一對輪胎能行使的最長路程是多少千公里?
【答案】(1)每名熟練工每日安裝![]() 輛自行車,每名新工人每日安裝
輛自行車,每名新工人每日安裝![]() 輛自行車;(2)
輛自行車;(2)![]() 或
或![]() 或
或![]() 或
或![]() ;(3)一對輪胎能行駛的最長路程是
;(3)一對輪胎能行駛的最長路程是![]() 千公里.
千公里.
【解析】
(1)設每名熟練工每日安裝![]() 輛自行車,每名新工人每日安裝
輛自行車,每名新工人每日安裝![]() 輛自行車,根據題意列出二元一次方程組即可求解;
輛自行車,根據題意列出二元一次方程組即可求解;
(2)設熟練工有![]() 名,得到方程求出m,n的關系,根據
名,得到方程求出m,n的關系,根據![]() 即可求解;
即可求解;
(3)假設一個輪胎用作前輪實驗使用![]() 千公里,用作后輪使用
千公里,用作后輪使用![]() 千公里,根據題意列出方程組即可求解.
千公里,根據題意列出方程組即可求解.
(1) 設每名熟練工每日安裝![]() 輛自行車,每名新工人每日安裝
輛自行車,每名新工人每日安裝![]() 輛自行車.
輛自行車.
由題意得![]() ,解得
,解得![]() ,
,
答:每名熟練工每日安裝![]() 輛自行車,每名新工人每日安裝
輛自行車,每名新工人每日安裝![]() 輛自行車.
輛自行車.
(2) 設熟練工有![]() 名,則
名,則![]() ,
,![]() ,
,![]() ,
,
![]() 或
或![]() 或
或![]() 或
或![]() .
.
(3) 假設一個輪胎用作前輪實驗使用![]() 千公里,用作后輪使用
千公里,用作后輪使用![]() 千公里,則
千公里,則
 ,則
,則![]() .
.
答:一對輪胎能行駛的最長路程是![]() 千公里.
千公里.


 計算高手系列答案
計算高手系列答案科目:初中數學 來源: 題型:
【題目】現有![]() 、
、![]() 兩種商品,已知買一件
兩種商品,已知買一件![]() 商品要比買一件
商品要比買一件![]() 商品少
商品少![]() 元,用
元,用![]() 元全部購買
元全部購買![]() 商品的數量與用
商品的數量與用![]() 元全部購買
元全部購買![]() 商品的數量相同.
商品的數量相同.
(1)求![]() 、
、![]() 兩種商品每件各是多少元?
兩種商品每件各是多少元?
(2)如果小亮準備購買![]() 、
、![]() 兩種商品共
兩種商品共![]() 件,總費用不超過
件,總費用不超過![]() 元,且不低于
元,且不低于![]() 元,問有幾種購買方案,哪種方案費用最低?
元,問有幾種購買方案,哪種方案費用最低?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BD⊥AC于點D,CE⊥AB于點E,BD與CE相交于點O,且BD=CE,連接AO.

(1)求證:△BOC是等腰三角形;
(2)求證:AO平分∠BAC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,反比例函數y=![]() (k≠0)的圖象過等邊三角形AOB的頂點A,已知點B(﹣2,0)
(k≠0)的圖象過等邊三角形AOB的頂點A,已知點B(﹣2,0)
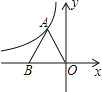
(1)求反比例函數的表達式;
(2)若要使點B在上述反比例函數的圖象上,需將△ABC向上平移多少個單位長度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△DEB中,已知AB=DE,還需添加兩個條件才能使△ABC≌△DEC,不能添加的一組條件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,平面直角坐標系xOy中,若A(0,4)、B(1,0)且以AB為直角邊作等腰Rt△ABC,∠CAB=90°,AB=AC.

(1)如圖1,求C點坐標;
(2)如圖2,在圖1中過C點作CD⊥x軸于D,連接AD,求∠ADC的度數;
(3)如圖3,點A在y軸上運動,以OA為直角邊作等腰Rt△OAE,連接EC,交y軸于F,試問A點在運動過程中S△AOB:S△AEF的值是否會發生變化?如果沒有變化,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com