
【題目】如圖,C為射線AB上一點,AB=30,AC比BC的![]() 多5,P,Q兩點分別從A,B兩點同時出發(fā).分別以2單位/秒和1單位/秒的速度在射線AB上沿AB方向運動,運動時間為t秒,M為BP的中點,N為QM的中點,以下結論:①BC=2AC;②AB=4NQ;③當PB=
多5,P,Q兩點分別從A,B兩點同時出發(fā).分別以2單位/秒和1單位/秒的速度在射線AB上沿AB方向運動,運動時間為t秒,M為BP的中點,N為QM的中點,以下結論:①BC=2AC;②AB=4NQ;③當PB=![]() BQ時,t=12,其中正確結論的個數(shù)是( )
BQ時,t=12,其中正確結論的個數(shù)是( )
![]()
A.0B.1C.2D.3
【答案】C
【解析】
根據(jù)AC比BC的![]() 多5可分別求出AC與BC的長度,然后分別求出當P與Q重合時,此時t=30s,當P到達B時,此時t=15s,最后分情況討論點P與Q的位置.
多5可分別求出AC與BC的長度,然后分別求出當P與Q重合時,此時t=30s,當P到達B時,此時t=15s,最后分情況討論點P與Q的位置.
解:設BC=x,
∴AC=![]() x+5
x+5
∵AC+BC=AB
∴x+![]() x+5=30,
x+5=30,
解得:x=20,
∴BC=20,AC=10,
∴BC=2AC,故①成立,
∵AP=2t,BQ=t,
當0≤t≤15時,
此時點P在線段AB上,
∴BP=AB﹣AP=30﹣2t,
∵M是BP的中點
∴MB=![]() BP=15﹣t
BP=15﹣t
∵QM=MB+BQ,
∴QM=15,
∵N為QM的中點,
∴NQ=![]() QM=
QM=![]() ,
,
∴AB=4NQ,
當15<t≤30時,
此時點P在線段AB外,且點P在Q的左側,
∴AP=2t,BQ=t,
∴BP=AP﹣AB=2t﹣30,
∵M是BP的中點
∴BM=![]() BP=t﹣15
BP=t﹣15
∵QM=BQ﹣BM=15,
∵N為QM的中點,
∴NQ=![]() QM=
QM=![]() ,
,
∴AB=4NQ,
當t>30時,
此時點P在Q的右側,
∴AP=2t,BQ=t,
∴BP=AP﹣AB=2t﹣30,
∵M是BP的中點
∴BM=![]() BP=t﹣15
BP=t﹣15
∵QM=BQ﹣BM=15,
∵N為QM的中點,
∴NQ=![]() QM=
QM=![]() ,
,
∴AB=4NQ,
綜上所述,AB=4NQ,故②正確,
當0<t≤15,PB=![]() BQ時,此時點P在線段AB上,
BQ時,此時點P在線段AB上,
∴AP=2t,BQ=t
∴PB=AB﹣AP=30﹣2t,
∴30﹣2t=![]() t,
t,
∴t=12,
當15<t≤30,PB=![]() BQ時,此時點P在線段AB外,且點P在Q的左側,
BQ時,此時點P在線段AB外,且點P在Q的左側,
∴AP=2t,BQ=t,
∴PB=AP﹣AB=2t﹣30,
∴2t﹣30=![]() t,
t,
t=20,
當t>30時,此時點P在Q的右側,
∴AP=2t,BQ=t,
∴PB=AP﹣AB=2t﹣30,
∴2t﹣30=![]() t,
t,
t=20,不符合t>30,
綜上所述,當PB=![]() BQ時,t=12或20,故③錯誤;
BQ時,t=12或20,故③錯誤;
故選:C.
![]()
![]()


 黎明文化寒假作業(yè)系列答案
黎明文化寒假作業(yè)系列答案 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數(shù)學 來源: 題型:
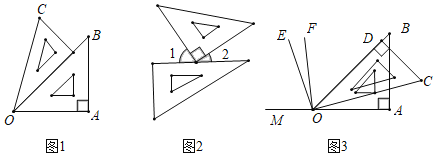
【題目】借助一副三角板,可以得到一些平面圖形
(1)如圖1,∠AOC= 度.由射線OA,OB,OC組成的所有小于平角的和是多少度?
(2)如圖2,∠1的度數(shù)比∠2度數(shù)的3倍還多30°,求∠2的度數(shù);
(3)利用圖3,反向延長射線OA到M,OE平分∠BOM,OF平分∠COM,請按題意補全圖(3),并求出∠EOF的度數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】用如圖1所示的曲尺形框框(有三個方向),可以套住圖2日歷中的三個數(shù),設被框住的三個數(shù)中(第一個框框住的最大的數(shù)為![]() 、第二個框框住的最大的數(shù)為
、第二個框框住的最大的數(shù)為![]() 、第三個框框住的最大的數(shù)為
、第三個框框住的最大的數(shù)為![]() )
)

(1)第一個框框住的三個數(shù)的和是: ,第二個框框住的三個數(shù)的和是: ,第三個框框住的三個數(shù)中的和是: ;
(2)這三個框框住的數(shù)的和分別能是81嗎?若能,則分別求出最大的數(shù)![]() 、
、![]() 、
、![]() .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
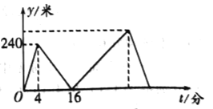
【題目】小瑩和小亮在筆直的公路上同起點、同終點、同方向勻速步行![]() 米,先到終點的人原地休息.已知小瑩先出發(fā)
米,先到終點的人原地休息.已知小瑩先出發(fā)![]() 分鐘,在整個步行過程中,兩人的距離
分鐘,在整個步行過程中,兩人的距離![]() (米)與小瑩出發(fā)的時間
(米)與小瑩出發(fā)的時間![]() (分)之間的關系如圖所示,下列結論:①小瑩的步行速度為
(分)之間的關系如圖所示,下列結論:①小瑩的步行速度為![]() 米/分;②小亮用
米/分;②小亮用![]() 分鐘追上小瑩;③小亮走完全程用了
分鐘追上小瑩;③小亮走完全程用了![]() 分鐘;④小亮到達終點時,小瑩離終點還有
分鐘;④小亮到達終點時,小瑩離終點還有![]() 米。其中正確的結論有( )
米。其中正確的結論有( )
A. ![]() 個B.
個B. ![]() 個C.
個C. ![]() 個D.
個D. ![]() 個
個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某中學要在一塊三角形花圃里種植兩種不同的花草,同時擬從A點修建一條小路到邊BC.
(1)若要使修建小路所用的材料最少,請在下圖中畫出小路AD;
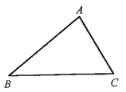
(2)若要使小路兩側種植不同花草的面積相等,請在下圖中畫出小路AE,其中E點滿足的條件是________,并說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AB、CD為⊙O的直徑,弦AE∥CD,連接BE交CD于點F,過點E作直線EP與CD的延長線交于點P,使∠PED=∠C.
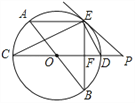
(1)求證:PE是⊙O的切線;
(2)求證:ED平分∠BEP.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
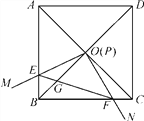
【題目】如圖,邊長為1的正方形ABCD的對角線AC,BD相交于點O,有直角∠MPN,使直角頂點P與點O重合,直角邊PM,PN分別與OA,OB重合,然后逆時針旋轉∠MPN,旋轉角為θ(0°<θ<90°),PM,PN分別交AB,BC于E,F(xiàn)兩點,連接EF交OB于點G,則下列結論:(1)EF=![]() OE;(2)S四邊形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=
OE;(2)S四邊形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=![]() OA;(4)在旋轉過程中,當△BEF與△COF的面積之和最大時,AE=
OA;(4)在旋轉過程中,當△BEF與△COF的面積之和最大時,AE=![]() ;(5)OG·BD=AE2+CF2,其中正確的是__.
;(5)OG·BD=AE2+CF2,其中正確的是__.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知,直線AB與直線CD相交于O,OB平分∠DOF.

(1)如圖,若∠BOF=40°,求∠AOC的度數(shù);
(2)作射線OE,使得∠COE=60°,若∠BOF=x°(![]() ),求∠AOE的度數(shù)(用含x的代數(shù)式表示).
),求∠AOE的度數(shù)(用含x的代數(shù)式表示).
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com