【題目】如圖，在平面直角坐標系中，點A的坐標為（2，3）且AO=BO，∠AOB=90°則點B的坐標為（ ）
A.（2，3）B.（-3，2）C.（-3，-2）D.（-2，3）
科目：初中數學 來源： 題型：
【題目】如圖，某中學有一塊四邊形的空地ABCD，學校計劃在空地上種植草皮，經測量∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m，若每平方米草皮需要200元，問學校需要投入多少資金買草皮？
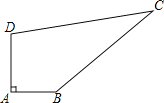
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】現有一項資助貧困生的公益活動由你來主持，每位參與者需交贊助費5元，活動規則如下：如圖是兩個可以自由轉動的轉盤，每個轉盤被分成6個相等的扇形，參與者轉動這兩個轉盤，轉盤停止后，指針各自指向一個數字，（若指針在分格線上，則重轉一次，直到指針指向某一數字為止），若指針最后所指的數字之和為12，則獲得一等獎，獎金20元；數字之和為9，則獲得二等獎，獎金10元；數字之和為7，則獲得三等獎，獎金為5元；其余均不得獎；此次活動所集到的贊助費除支付獲獎人員的獎金外，其余全部用于資助貧困生的學習和生活；
（1）分別求出此次活動中獲得一等獎、二等獎、三等獎的概率；
（2）若此次活動有2000人參加，活動結束后至少有多少贊助費用于資助貧困生？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是小章為學校舉辦的數學文化節沒計的標志，在△ABC中，∠ACB＝90°，以△ABC的各邊為邊作三個正方形，點G落在HI上，若AC+BC＝6，空自部分面積為10.5，則陰影部分面積為______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們定義：如圖1，在
中，把AB繞點A順時針旋轉
得到
，把AC繞點A逆時針旋轉
得到
，連接
當
時，我們稱
是的“旋補三角形”， 邊上的中線AD叫做的“旋補中線”，點A叫做“旋補中心”．
特例感知：
在圖2，圖3中，是的“旋補三角形”，AD是的“旋補中線”．
如圖2，當為等邊三角形時，AD與BC的數量關系為
______BC；
如圖3，當
，
時，則AD長為______．
猜想論證：
在圖1中，當為任意三角形時，猜想AD與BC的數量關系，并給予證明．
拓展應用
如圖4，在四邊形ABCD，
，
，
，
，
在四邊形內部是否存在點P，使
是
的“旋補三角形”？若存在，給予證明，并求的“旋補中線”長；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
中，
，以點O為圓心的
經過AB的中點C，連接OC，直線AO與相交于點E，D，OB交于點F，P是
的中點，連接CE，CF，BP．
求證：AB是的切線；
若
，則
當
______時，四邊形OECF是菱形；
當______時，四邊形OCBP是正方形
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y＝
x與雙曲線y＝
(k>0，x>0)交于點A，將直線y＝x向上平移4個單位長度后，與y軸交于點C，與雙曲線y＝ (k>0，x>0)交于點B，若OA＝3BC，則k的值為( )
A. 3 B. 6 C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】著名的恩施大峽谷（A）和世界級自然保護區星斗山（B）位于筆直的滬渝高速公路X同側，AB＝50km，A、B到直線X的距離分別為10km和40km，要在滬渝高速公路旁修建一服務區P，向A、B兩景區運送游客．小民設計了兩種方案，圖1是方案一的示意圖（AP與直線X垂直，垂足為P），P到A、B的距離之和S1＝PA+PB，圖2是方案二的示意圖（點A關于直線X的對稱點是A'，連接BA′交直線X于點P），P到A、B的距離之和S2＝PA+PB
（1）S1＝_____km．S2＝_____km．
（2）PA+PB的最小值為_____km．
（3）擬建的恩施到張家界高速公路與滬渝高速公路垂直，建立如圖3所示的直角坐標系，B到直線的距為30km，請你在X旁和P旁各修建一服務區P、Q，使P、A、B、Q組成的四邊形的周長最小，（用尺畫出點P和點Q的位置）這個最小值為_____km．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，∠E＝∠F＝90°，∠B＝∠C，AE＝AF，結論：①EM＝FN；②AF
∥EB；③∠FAN＝∠EAM；④△ACN≌△ABM
其中正確的有 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
