
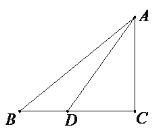
【題目】如圖,在ΔABC中,∠C=90°,點D在BC上,BD=4,AD=BC,cos∠ADC=![]() .
.
(1)求DC的長;
(2)求sinB的值.
【答案】(1)CD=6;(1)sinB= ![]() .
.
【解析】
(1)根據cos∠ADC=![]() ,就是已知CD:AD=3:5,因而可以設CD=3x,AD=5x,AC=4x.根據BD=4,就可以得到關于x的方程,就可以求出x,求出CD的長度;
,就是已知CD:AD=3:5,因而可以設CD=3x,AD=5x,AC=4x.根據BD=4,就可以得到關于x的方程,就可以求出x,求出CD的長度;
(2)在Rt△ABC中,先利用勾股定理求出AB,再根據正弦函數的定義即可求出sinB的值.
解:(1)在直角△ACD中,cos∠ADC=![]() =
=![]() ,
,
因而可以設CD=3x,AD=5x,
根據勾股定理得到AC=4x,則BC=AD=5x,
∵BD=4,∴5x-3x=4,
解得x=2,
因而BC=10,AC=8,
CD=6;
(2)在直角△ABC中,根據勾股定理得到AB=2![]() ,
,
∴sinB=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
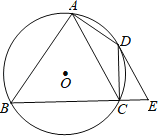
【題目】如圖,四邊形ABCD內接于⊙O,∠BAD=90°,點E在BC的延長線上,且∠DEC=∠BAC.
(1)求證:DE是⊙O的切線;
(2)若AC∥DE,當AB=8,CE=2時,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小明在家鄉的樓頂上![]() 處測得池塘的一端
處測得池塘的一端![]() 處的俯角為
處的俯角為![]() ,測得池塘
,測得池塘![]() 處的俯角
處的俯角![]() ,
,![]() 、
、![]() 、
、![]() 三點在同一水平直線上.已知樓高
三點在同一水平直線上.已知樓高![]() 米,求池塘寬
米,求池塘寬![]() 為多少米?(參考數據:
為多少米?(參考數據:![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() .結果保留一位小數.)
.結果保留一位小數.)

查看答案和解析>>
科目:初中數學 來源: 題型:
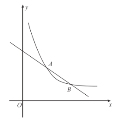
【題目】如圖,在平面直角坐標系![]() 中,一次函數
中,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() (
(![]() )的圖象交于
)的圖象交于![]() ,
,![]() 兩點.
兩點.
(1)求![]() 的值;
的值;
(2)求出一次函數與反比例函數的表達式;
(3)過點![]() 作
作![]() 軸的垂線,與直線
軸的垂線,與直線![]() 和函數
和函數![]() (
(![]() )的圖象的交點分別為點
)的圖象的交點分別為點![]() ,
,![]() ,當點
,當點![]() 在點
在點![]() 下方時,寫出
下方時,寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() (
(![]() ).
).
(1)求出二次函數圖象的對稱軸;
(2)若該二次函數的圖象經過點![]() ,且整數
,且整數![]() ,
,![]() 滿足
滿足![]() ,求二次函數的表達式;
,求二次函數的表達式;
(3)對于該二次函數圖象上的兩點![]() ,
,![]() ,設
,設![]() ,當
,當![]() 時,均有
時,均有![]() ,請結合圖象,直接寫出
,請結合圖象,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們做如下的規定:如果一個三角形在運動變化時保持形狀和大小不變,則把這樣的三角形稱為三角形板.
把兩塊邊長為4的等邊三角形板![]() 和
和![]() 疊放在一起,使三角形板
疊放在一起,使三角形板![]() 的頂點
的頂點![]() 與三角形板
與三角形板![]() 的AC邊中點
的AC邊中點![]() 重合,把三角形板
重合,把三角形板![]() 固定不動,讓三角形板
固定不動,讓三角形板![]() 繞點
繞點![]() 旋轉,設射線
旋轉,設射線![]() 與射線
與射線![]() 相交于點M,射線
相交于點M,射線![]() 與線段
與線段![]() 相交于點N.
相交于點N.
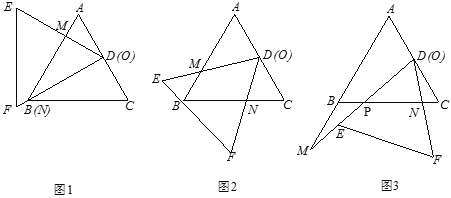
(1)如圖1,當射線![]() 經過點
經過點![]() ,即點N與點
,即點N與點![]() 重合時,易證△ADM∽△CND.此時,AM·CN= .
重合時,易證△ADM∽△CND.此時,AM·CN= .
(2)將三角形板![]() 由圖1所示的位置繞點
由圖1所示的位置繞點![]() 沿逆時針方向旋轉,設旋轉角為
沿逆時針方向旋轉,設旋轉角為![]() .其中
.其中![]() ,問AM·CN的值是否改變?說明你的理由.
,問AM·CN的值是否改變?說明你的理由.
(3)在(2)的條件下,設AM= x,兩塊三角形板重疊面積為![]() ,求
,求![]() 與
與![]() 的函數關系式.(圖2,圖3供解題用)
的函數關系式.(圖2,圖3供解題用)
查看答案和解析>>
科目:初中數學 來源: 題型:
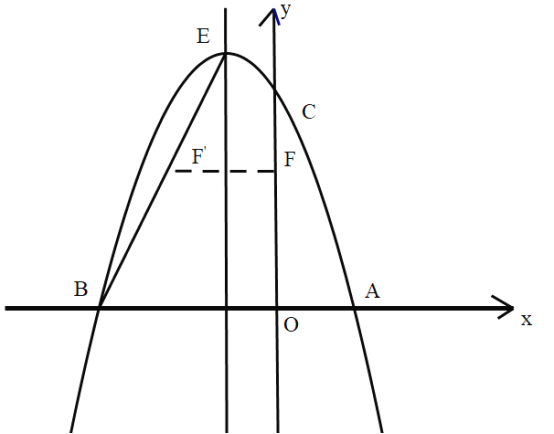
【題目】如圖,二次函數![]() 的圖像與
的圖像與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,直線l是拋物線的對稱軸,
,直線l是拋物線的對稱軸,![]() 是拋物線的頂點.
是拋物線的頂點.
(1)求拋物線的解析式及頂點![]() 的坐標;
的坐標;
(2)如圖,連接![]() ,線段
,線段![]() 上的點
上的點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 恰好在線段
恰好在線段![]() 上,求點
上,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
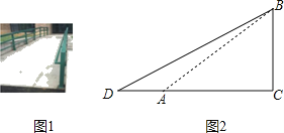
【題目】圖1是無障礙通道,圖2是其截面示意圖,已知坡角∠BAC=30°,斜坡AB=4m,∠ACB=90°.現要對坡面進行改造,使改造后的坡角∠BDC=26.5°,需要把水平寬度AC增加多少m(結果精確到0.1)?(參考數據:![]() ≈1.73,sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50)
≈1.73,sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50)
查看答案和解析>>
科目:初中數學 來源: 題型:
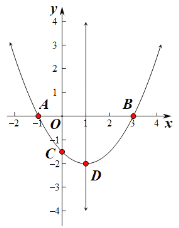
【題目】拋物線![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() ,交
,交![]() 軸的負半軸于
軸的負半軸于![]() ,頂點為
,頂點為![]() .下列結論:①
.下列結論:①![]() ;②
;②![]() ;③當
;③當![]() 時,
時,![]() ;④當
;④當![]() 是等腰直角三角形時,則
是等腰直角三角形時,則![]() ;⑤若
;⑤若![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的兩個根,且
的兩個根,且![]() ,則
,則![]() .其中錯誤的有( )個.
.其中錯誤的有( )個.
A.5B.4C.3D.2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com