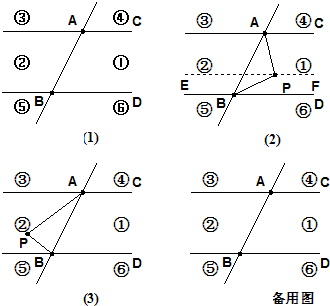
26、如圖1，直線AC∥BD，直線AC、BD及直線AB把平面分成（1）、（2）、（3）、（4）、（5）、（6）六個部分．點P是其中的一個動點，連接PA、PB，觀察∠APB、∠PAC、∠PBD三個角．規定：直線AC、BD、AB上的各點不屬于（1）、（2）、（3）、（4）、（5）、（6）六個部分中的任何一個部分．
當動點P落在第（1）部分時，可得：∠APB=∠PAC+∠PBD，請閱讀下面的解答過程，并在相應的括號內填注理由
解：過點P作EF∥AC，如圖2
因為AC∥BD（已知），EF∥AC（所作），
所以EF∥BD
（平行線的傳遞性）
．
所以∠BPE=∠PBD
（兩直線平行，內錯角相等）
．
同理∠APE=∠PAC．
因此∠APE+∠BPE=∠PAC+∠PBD
（等量代換）
，
即∠APB=∠PAC+∠PBD．
（1）當動點P落在第（2）部分時，∠APB、∠PAC、∠PBD之間的關系是怎樣的？請直接寫出∠APB、∠PAC、∠PBD之間滿足的關系式，不必說明理由．
（2）當動點P在第（3）部分時，∠APB、∠PAC、∠PBD之間的關系是怎樣的？請直接寫出相應的結論．
（3）當動點P在第（4）部分時，∠APB、∠PAC、∠PBD之間的關系是怎樣的？請直接寫出相應的結論．
一課一練一本通系列答案
浙江之星學業水平測試系列答案
