
【題目】如圖![]() ,已知
,已知![]() ,
,![]() 在
在![]() 的右倒,
的右倒,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() 所在直線交于點
所在直線交于點![]() ,
,![]() .
.
(1)求![]() 的度數.
的度數.
(2)若![]() ,求
,求![]() 的度數(用含
的度數(用含![]() 的代數式表示).
的代數式表示).
(3)將線段![]() 沿
沿![]() 方向平移,使得點
方向平移,使得點![]() 在點
在點![]() 的右側,其他條件不變,在圖
的右側,其他條件不變,在圖![]() 中畫出平移后的圖形,并判斷
中畫出平移后的圖形,并判斷![]() 的度數是否發生改變?若改變,求出它的度數(用含
的度數是否發生改變?若改變,求出它的度數(用含![]() 的式子表示);若不改變,請說明理由.
的式子表示);若不改變,請說明理由.


圖1 圖2
科目:初中數學 來源: 題型:
【題目】一文體用品商店為吸引中學生顧客,在店內出示了一道數學題,凡是能正確解答這道題的,店內商品一律給該生9折優惠或每購滿10元立減3元(不足10元部分不減)優惠方式.題目是這樣的:購一個筆盒和2個羽毛球共需26元,買2個筆盒和一個羽毛球共需37元,
(1)請列方程或方程組解答商家提出的問題;問:筆盒與羽毛球的單價各是多少元?
(2)一位同學回答對了問題,他想購買羽毛球和筆盒各一個,請列舉能享受到優惠的購買方式,并幫助他選擇一種最優惠的購買方式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙![]() 與菱形
與菱形![]() 在平面直角坐標系中,點
在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() 點
點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在
在![]() 軸上,且點
軸上,且點![]() 在點
在點![]() 的右側.
的右側.


(![]() )求菱形
)求菱形![]() 的周長.
的周長.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 軸向右以每秒
軸向右以每秒![]() 個單位長度的速度平移,菱形
個單位長度的速度平移,菱形![]() 沿
沿![]() 軸向左以每秒
軸向左以每秒![]() 個單位長度的速度平移,設菱形移動的時間為(
個單位長度的速度平移,設菱形移動的時間為(![]() 秒),當⊙
秒),當⊙![]() 與
與![]() 相切,且切點為
相切,且切點為![]() 的中點時,連接
的中點時,連接![]() ,求
,求![]() 的值及
的值及![]() 的度數.
的度數.
(![]() )在(
)在(![]() )的條件下,當點
)的條件下,當點![]() 與
與![]() 所在的直線的距離為
所在的直線的距離為![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣![]() +bx+4與x軸相交于A、B兩點,與y軸相交于點C,若已知A點的坐標為(﹣2,0).
+bx+4與x軸相交于A、B兩點,與y軸相交于點C,若已知A點的坐標為(﹣2,0).
(1)求拋物線的解析式;
(2)連接AC、BC,求線段BC所在直線的解析式;
(3)在拋物線的對稱軸上是否存在點P,使△ACP為等腰三角形?若存在,求出符合條件的P點坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形EFGH的頂點E,G分別在菱形ABCD的邊AD,BC上,頂點F,H在菱形ABCD的對角線BD上.

(1)求證:BG=DE;
(2)若E為AD中點,FH=2,求菱形ABCD的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:有一組對角是直角的四邊形叫做“準矩形”;有兩組鄰邊(不重復)相等的四邊形叫做“準菱形”.如圖①,在四邊形ABCD中,若∠A=∠C=90°,則四邊形ABCD是“準矩形”;如圖②,在四邊形ABCD中,若AB=AD,BC=DC,則四邊形ABCD是“準菱形”.
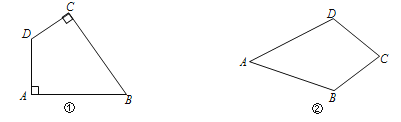
(1)如圖,在邊長為1的正方形網格中,A、B、C在格點(小正方形的頂點)上,請分別在圖③、圖④中畫出“準矩形”ABCD和“準菱形”ABCD′.(要求:D、D′在格點上);

(2)下列說法正確的有 ;(填寫所有正確結論的序號)
①一組對邊平行的“準矩形”是矩形;②一組對邊相等的“準矩形”是矩形;
③一組對邊相等的“準菱形”是菱形;④一組對邊平行的“準菱形”是菱形.
(3)如圖⑤,在△ABC中,∠ABC=90°,以AC為一邊向外作“準菱形”ACEF,且AC=EC,AF=EF,AE、CF交于點D.
①若∠ACE=∠AFE,求證:“準菱形”ACEF是菱形;
②在①的條件下,連接BD,若BD=![]() ,∠ACB=15°,∠ACD=30°,請直接寫出四邊形ACEF的面積.
,∠ACB=15°,∠ACD=30°,請直接寫出四邊形ACEF的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把一張長方形紙片ABCD折疊起來,使其對角頂點A與C重合,D與G重合.若長方形的長BC為8,寬AB為4,求:
(1)CF的長;
(2)求三角形GED的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點![]() 為正方形
為正方形![]() 的邊
的邊![]() 上任意一點,在正方形內部做等腰直角
上任意一點,在正方形內部做等腰直角![]() .
.


(1)如圖1,若![]() ,則
,則![]() _________(請直接寫出答案)
_________(請直接寫出答案)
(2)作![]() 關于
關于![]() 的對稱點
的對稱點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() .
.
①補全圖形1;
②證明:四邊形ECHF為平行四邊形.
(3)在(2)的條件下,連接![]() ,請直接寫出
,請直接寫出![]() 和
和![]() 之間的數量關系.
之間的數量關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com