
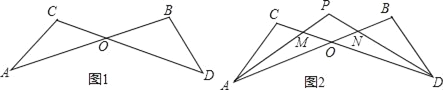
【題目】如圖1,已知線段AB、CD相交于點O,連接AC、BD,則我們把形如這樣的圖形稱為“8字型”.
(1)求證:∠A+∠C=∠B+D;
(2)如圖2,若∠CAB和∠BDC的平分線AP和DP相交于點P,且與CD、AB分別相交于點M、N.
①以線段AC為邊的“8字型”有 個,以點O為交點的“8字型”有 個;
②若∠B=100°,∠C=120°,求∠P的度數;
③若角平分線中角的關系改為“∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB”,試探究∠P與∠B、∠C之間存在的數量關系,并證明理由.
∠CDB”,試探究∠P與∠B、∠C之間存在的數量關系,并證明理由.
【答案】(1)證明見解析;(2)①3, 4;②∠P=110°;③3∠P=∠B+2∠C,理由見解析.
【解析】
(1)由三角形內角和得到∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,由對頂角相等,得到∠AOC=∠BOD,因而∠A+∠C=∠B+∠D;
(2)①以線段AC為邊的“8字形”有3個,以O為交點的“8字形”有4個;
②根據(1)的結論,以M為交點“8字型”中,∠P+∠CDP=∠C+∠CAP,以N為交點“8字型”中,∠P+∠BAP=∠B+∠BDP,兩等式相加得到2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,由AP和DP是角平分線,得到∠BAP=∠CAP,∠CDP=∠BDP,從而∠P=![]() (∠B+∠C),然后將∠B=100,∠C=120代入計算即可;
(∠B+∠C),然后將∠B=100,∠C=120代入計算即可;
③與②的證明方法一樣得到3∠P=∠B+2∠C.
解:(1)在圖1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)解:①以線段AC為邊的“8字型”有3個:



以點O為交點的“8字型”有4個:




②以M為交點“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N為交點“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分別平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,
∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,
∴∠P=![]() (∠B+∠C)=
(∠B+∠C)=![]() (100°+120°)=110°;
(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,
∠CDB,
∴∠BAP=![]() ∠CAB,∠BDP=
∠CAB,∠BDP=![]() ∠CDB,
∠CDB,
以M為交點“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N為交點“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP=![]() (∠CDB﹣∠CAB),
(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP=![]() (∠CDB﹣∠CAB).
(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B,
∴3∠P=∠B+2∠C.
故答案為:(1)證明見解析;(2)①3, 4;②∠P=110°;③3∠P=∠B+2∠C,理由見解析.


科目:初中數學 來源: 題型:
【題目】“綠色出行,低碳健身”已成為廣大市民的共識.為方便市民出行,東臺市推出了公共自行車系統,收費以小時為單位,每次使用不超過1小時的免費,超過1小時后,不足1小時的部分按1小時收費.小紅同學通過調查得知,自行車使用時間為3小時,收費2元;使用時間為4小時,收費3元.她發現當使用時間超過1小時后用車費用與使用時間之間存在一次函數的關系.
(1)設使用自行車的費用為![]() 元,使用時間為
元,使用時間為![]() 小時(
小時(![]() 為大于1的整數),求
為大于1的整數),求![]() 與
與![]() 的函數解析式;
的函數解析式;
(2)若小紅此次使用公共自行車5小時,則她應付多少元費用?
(3)若小紅此次使用公共自行車付費6元,求她所使用自行車的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形網格中,每個小正方形的邊長均為1個單位長度,△ABC的三個頂點的位置如圖所示,現將△ABC平移,使點A變換為點A′,點B′、C′分別是B、C的對應點.

(1)請畫出平移后的△A′B′C′,并求△A′B′C′的面積;
(2)若連接AA′,CC′,則這兩條線段之間的關系是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某次海上軍事學習期間,我軍為確保△OBC海域內的安全,特派遣三艘軍艦分別在O、B、C處監控△OBC海域,在雷達顯示圖上,軍艦B在軍艦O的正東方向80海里處,軍艦C在軍艦B的正北方向60海里處,三艘軍艦上裝載有相同的探測雷達,雷達的有效探測范圍是半徑為r的圓形區域.(只考慮在海平面上的探測) 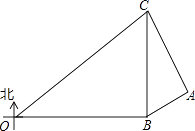
(1)若三艘軍艦要對△OBC海域進行無盲點監控,則雷達的有效探測半徑r至少為多少海里?
(2)現有一艘敵艦A從東部接近△OBC海域,在某一時刻軍艦B測得A位于北偏東60°方向上,同時軍艦C測得A位于南偏東30°方向上,求此時敵艦A離△OBC海域的最短距離為多少海里?
(3)若敵艦A沿最短距離的路線以20 ![]() 海里/小時的速度靠近△OBC海域,我軍軍艦B沿北偏東15°的方向行進攔截,問B軍艦速度至少為多少才能在此方向上攔截到敵艦A?
海里/小時的速度靠近△OBC海域,我軍軍艦B沿北偏東15°的方向行進攔截,問B軍艦速度至少為多少才能在此方向上攔截到敵艦A?
查看答案和解析>>
科目:初中數學 來源: 題型:
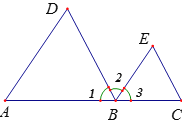
【題目】如圖,A、B、C在同一直線上,
(1)若∠A=∠3,依據__________,可得______∥_______;
(2)若∠______=∠______,則依據內錯角相等,兩直線平行,可得DB∥EC;
(3)若∠______+∠_______=180°,則AD∥BE,依據是____________;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A(1,6)B(n,﹣2)是一次函數y=kx+b的圖象和反比例函數y= ![]() 的圖象的兩個交點,直線與y軸交于C點.
的圖象的兩個交點,直線與y軸交于C點. 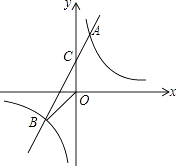
(1)求反比例函數和一次函數的表達式;
(2)求△BOC的面積;
(3)直接寫出不等式kx+b﹣ ![]() >0的解集.
>0的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com