如圖，在△ABC中，以AC邊為直徑的⊙O交BC于點D，在劣弧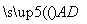
上取一點E使∠EBC = ∠DEC，延長BE依次交AC于G，交⊙O于H.
(1)求∠AGB的度數；
(2)若∠ABC= 45°，⊙O的直徑等于17，BD =15，求CE的長.
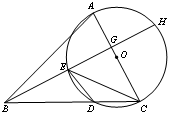
證明：（1）連結AD
∵∠DAC = ∠DEC ∠EBC = ∠DEC
∴∠DAC = ∠EBC
又∵AC是⊙O的直徑 ∴∠ADC=90°
∴∠DCA+∠DAC=90° ∴∠EBC+∠DCA = 90°
∴∠BGC=180°–（∠EBC+∠DCA) = 180°–90°=90°
∴∠AGB=90°
（2）∵∠BDA=180°–∠ADC = 90° ∠ABC = 45° ∴∠BAD = 45°
∴BD = AD
∵BD =15 ∴AD =15
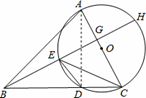又∵∠ADC = 90° AC =17
∴由勾股定理 DC=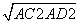 
=8
∴BC=BD+DC=8+15=23
∵∠EBC=∠DEC，∠BCE=∠ECD，
∴△BCE∽△ECD
∴
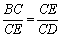
∴CE=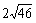
科目：初中數學 來源： 題型：
我市某中學九年級學生對市民“創建精神文明城市“知曉率采取隨機抽樣的方法進行問卷調查，問卷調查的結果劃分為“非常了解”、“比較了解”、“基本了解”、“不太了解“、“從未聽說”五個等級，統計后的數據整理如下表：
| 等級 | 非常了解 | 比較了解 | 基本了解 | 不太了解 | 從未聽說 |
| 頻數 | 40 | 60 | 48 | 36 | 16 |
| 頻率 | 0.2 | m | 0.24 | 0.18 | 0.08 |
（1）本次問卷調查抽取的樣本容量為 ，表中m的值為 ；
（2）根據表中的數據計算等級為“非常廣解”的頻數在扇形統計圖中所對應扇形的圓心角的度數；
（3）根據上述統計結果，請你對政府相關部門提出一句話建議．
查看答案和解析>>
科目：初中數學 來源： 題型：
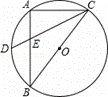
如圖,Rt△ABC內接于⊙O，BC為直徑，AB=4，AC=3，D是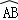
的中點，CD與AB的交點為E，則
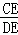等于（ ）
|
| A． | 4 | B． | 3.5 | C． | 3 | D． | 2.8 |
查看答案和解析>>
科目：初中數學 來源： 題型：
一個不透明的口袋中有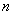
個小球，其中兩個是白球，其余為紅球，這些球的形狀、大小、質地等完全相同，從袋中隨機地取出一個球，它是紅球的概率是
．
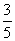(1)求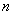的值；
(2)把這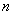個球中的兩個標號為1，其余分別標號為2，3，…，
，隨機地取出一個小球后不放回，再隨機地取出一個小球，請用畫樹狀圖或列表的方法求第二次取出小球標號大于第一次取出小球標號的概率．
(3)在第(2)小題中若把兩個標號為1的球分給甲、乙、丙三位同學，則甲乙各得一球的概率是多少？（直接寫出答案）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
>0）過A(-3,y1)、B(-7,,y2) 、C(4,y3)三點，把y1 、y2 、y3從小到大的順序排列為 
的解集是
，則（ ） 
≤
B．
C．
D．
三點可以確定一個圓時，
需要滿足的條件 ． 
的自變量
的取值范圍是( ) 
D．