
【題目】如圖,在△ABC中,AB=AC,點D、E、F分別在BC、AB、AC邊上,且BE=CF,AD+EC=AB.
(1)求證:△DEF是等腰三角形;
(2)當∠A=40°時,求∠DEF的度數;
(3)△DEF可能是等腰直角三角形嗎?為什么?
(4)請你猜想:當∠A為多少度時,∠EDF+∠EFD=120°,并請說明理由.

【答案】(1)證明見解析;(2)∠DEF=70°; (3)△DEF不可能是等腰直角三角形,理由見解析;(4)當∠A=60°時,∠EDF+∠EFD=120°,理由見解析.
【解析】
(1)首先根據條件證明△DBE≌△ECF,根據全等三角形的性質可得DE=FE,進而可得到△DEF是等腰三角形;
(2)由(1)中的全等得出∠BDE=∠CEF,再由角之間的轉化,從而可求解∠DEF的大小;(3)由于AB=AC,可得∠B=∠C≠90°=∠DEF,從而可確定其不可能是等腰直角三角形;
(4)先猜想出∠A的度數,則可得∠EDF+∠EFD=120°,根據前面的推導過程知∠EDF+∠EFD=120°時,∠DEF=60°,再由∠B=∠DEF以及等腰三角形的性質繼而推得猜想的正確性.
(1)∵AB=AC,
∴∠B=∠C,
∵AD+EC=AB,AB=AD+BD,
∴BD=CE,
在△BDE和△CEF中,
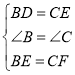 ,
,
∴△BDE≌△CEF(SAS)
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
由(1)知△BDE≌△CEF,
則∠BDE=∠CEF,
∴∠DEF=∠B,
∵∠A=40°,
∴∠B=∠C=![]() =70°,
=70°,
∴∠DEF=70°;
(3)△DEF不可能是等腰直角三角形,
∵AB=AC,
∴∠B=∠C≠90°,
由(2)知∠DEF=∠B,
∴∠DEF=∠B≠90°,
∴△DEF不可能是等腰直角三角形;
(4)當∠A=60°時,∠EDF+∠EFD=120°,
理由是:當∠EDF+∠EFD=120°時,
則∠DEF=180°-120°=60°,
∴∠B=∠DEF=60°,
∴∠A=180°-∠B-∠C=180°-60°-60°=60°,
∴當∠A=60°時,∠EDF+∠EFD=120°.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:初中數學 來源: 題型:
【題目】為弘揚中華傳統文化,我市某中學決定根據學生的興趣愛好組建課外興趣小組,因此學校隨機抽取了部分同學的興趣愛好進行調查,將收集的數據整理并繪制成下列兩幅統計圖,請根據圖中的信息,完成下列問題:
(1)學校這次調查共抽取了 名學生;
(2)補全條形統計圖;
(3)在扇形統計圖中,“戲曲”所在扇形的圓心角度數為 ;
(4)設該校共有學生2000名,請你估計該校有多少名學生喜歡書法?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,O為坐標原點,四邊形OABC為矩形,A(10,0),C(0,4),點D是OA的中點,點P在BC上運動,當△ODP是腰長為5的等腰三角形時,則P點的坐標為( )

A. (3,4)或(2,4) B. (2,4)或(8,4)
C. (3,4)或(8,4) D. (3,4)或(2,4)或(8,4)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在生活中,人們經常通過一些標志性建筑確定位置,在數學中往往也是這樣.
(1)將正整數如圖1的方式進行排列:

小明同學通過仔細觀察,發現每一行第一列的數字有一定的規律,所以每一行第一列的數字可以作為標志數,于是他認為第七行第一列的數字是 ,第7行、第5列的數字是 .
(2)方法應用
觀察下面一列數:1,﹣2,3,﹣4,5,﹣6,7,…并將這列數按照如圖2方式進行排列:
按照上述方式排列下去,
問題1:第10行從左邊數第9個數是 ;
問題2:第n行有 個數;(用含n的代數式表示)
問題3:數字2019在第 行,從左邊數第 個數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織七年級學生體育健康抽測,(1)班25名學生的成績(滿分為100分)統計如下:
90,74,88,65,98,76,81,42,85,70,55,80,95,88,72,87,61,56,76,66,78,72,82,63,100.
(1)90分及以上為A級,75-89分為B級,60-74分為C級,60分以下為D級,請把下面表格補充完整,并將圖中的條形圖補充完整;
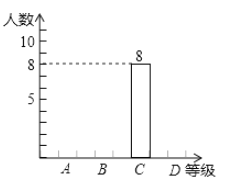
等級 | A | B | C | D |
人數 | 8 |
(2)該校七年級共有1000名學生,如果60分以上為合格,請估計七年級有多少人合格?
(3)請選擇合適的統計圖表示出抽測中每一個等級的人數占總人數的百分比.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰△ABC 中,AB=AC,中線 BD 將這個三角形的周長分成 15 和 18 兩部分, 則這個三角形底邊的長為( )
A. 9B. 13C. 9 或 13D. 10 或 12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“階梯水價”充分發揮市場、價格因素在水資源配置、水需求調節等方面的作用,拓展了水價上調的空間,增強了企業和居民的節水意識,避免了水資源的浪費.階梯式計量水價將水價分為兩段或者多段,每一分段都有一個保持不變的單位水價,但是單位水價會隨著耗水量分段而增加.某地“階梯水價”收費標準如下表(按月計算):
用水量 (單位:m3 ) | 單價(元/m3 ) |
不超出 | 2 |
超出 | 3 |
超出 | 5 |
例如:該地區某戶居民3月份用水![]() m3,則應交水費為
m3,則應交水費為![]() (元
(元![]() .
.
根據上表的內容解答下列問題:
(1)用戶甲5月份用水16 m3,則該用戶5月份應交水費多少元?
(2)用戶乙5月份交水費50元,則該用戶5月份的用水量為多少m3?
(3) 用戶丙5、6兩個月共用水![]() m3,其中6月份用水量超過了
m3,其中6月份用水量超過了![]() m3,設5月份用水
m3,設5月份用水![]() m3,請用含
m3,請用含![]() 的式子表示該戶居民5、6兩個月共交的水費.
的式子表示該戶居民5、6兩個月共交的水費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB//CD,

(1) 求∠1+∠2+∠3的度數.
(2) ∠1+∠2+∠3+∠4 = .
根據以上的規律求∠1+∠2+∠3+…+∠n = .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com