
【題目】下面是小蕓設計的“過圓外一點作已知圓的切線”的尺規作圖過程.
已知:⊙O 及⊙O 外一點 P.
求作:⊙O 的一條切線,使這條切線經過點 P.
作法:①連接 OP,作 OP 的垂直平分線 l,交 OP 于點 A;
②以 A 為圓心,AO 為半徑作圓,交⊙O 于點 M;
③作直線 PM,則直線 PM 即為⊙O 的切線.

根據小蕓設計的尺規作圖過程,
(1)使用直尺和圓規,補全圖形;(保留作圖痕跡)
(2)完成下面的證明:
證明:連接 OM,
由作圖可知,A 為 OP 中點,
∴OP 為⊙A 直徑,
∴∠ =90°( )(填推理的依據)
即 OM⊥PM.
又∵點 M 在⊙O 上,
∴PM 是⊙O 的切線.( )(填推理的依據)
【答案】(1)見解析;(2)OMP;直徑所對的圓周角是直角;經過半徑的外端并且垂直于這條半徑的直線是圓的切線.
【解析】
(1)根據作圖步驟利用尺規作圖可得;
(2)①根據“直徑所對圓周角是直角”可得;②根據“經過半徑的外端點,并且垂直于這條半徑的直線是圓的切線”可得.
解:(1)補全圖形,如圖所示:

(2)證明:連接OM,
由作圖可知,A為OP中點,
∴OP為⊙A直徑,
∴∠OMP=90°,(直徑所對的圓周角是直角),
即OM⊥PM.
又∵點M在⊙O上,
∴PM是⊙O的切線.(經過半徑的外端并且垂直于這條半徑的直線是圓的切線),
故答案為:OMP;直徑所對的圓周角是直角;經過半徑的外端并且垂直于這條半徑的直線是圓的切線.


科目:初中數學 來源: 題型:
【題目】草莓是云南多地盛產的一種水果,今年某水果銷售店在草莓銷售旺季試銷售成本為每千克18元的草莓,規定試銷期間銷售單價不低于成本單價,也不高于每千克40元.經試銷發現,銷售量y(kg)與銷售單價x(元/kg)符合一次函數關系,如圖是y與x的函數關系圖象.
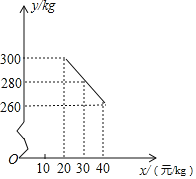
(1)求y與x的函數解析式;
(2)設該水果銷售店試銷草莓獲得的利潤為W元,求W的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人加工同一種零件,甲每天加工的數量是乙每天加工數量的 1.5 倍,兩人各加工 600 個這種零件,甲比乙少用 5 天.
(1)求甲、乙兩人每天各加工多少個這種零件?
(2)已知甲、乙兩人加工這種零件每天的加工費分別是 150 元和 120 元,現有 3000 個這種零件的加工任務,甲單獨加工一段時間后另有安排,剩余任務由乙單獨完成.如果總加工費不超過 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩車分別從A,B兩地相向勻速行駛,甲車先出發兩小時,甲車到達B地后立即調頭,并保持原速度與乙車同向行駛,乙車到達A地后,繼續保持原速向遠離B的方向行駛,經過一段時間后兩車同時到達C地,設兩車之間的距離為y(干米),甲車行駛的時間為x小時,y與x之間的函數圖象如圖所示,則當甲車重返A地時,乙車距離C地________千米.
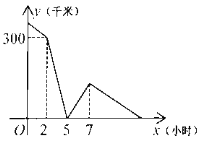
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系xoy中,二次函數![]() 的圖象與x軸的交點為A,B,頂點為C,點D為點C關于x軸的對稱點,過點A作直線l:
的圖象與x軸的交點為A,B,頂點為C,點D為點C關于x軸的對稱點,過點A作直線l:![]() 交BD于點E,連接BC的直線交直線l于K點.
交BD于點E,連接BC的直線交直線l于K點.
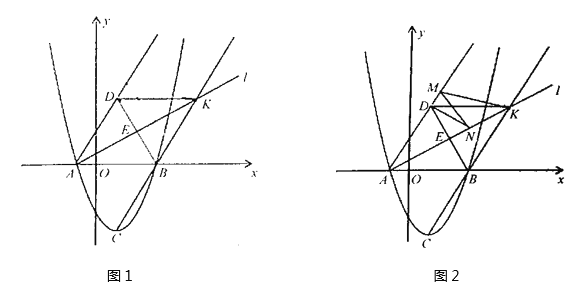
(1)問:在四邊形ABKD內部是否存在點P,使它到四邊形ABKD四邊的距離都相等?
若存在,請求出點P的坐標;若不存在,請說明理由;
(2)若M,N分別為直線AD和直線l上的兩個動點,連結DN,NM,MK,如圖2,求DN+NM+MK和的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某區初二年級數學學科期末質量監控情況,進行了抽樣調查,過程如下,請將有關問題補充完整.
收集數據:
隨機抽取甲乙兩所學校的 20 名學生的數學成績進行
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述數據 :
按如下數據段整理、描述這兩組數據
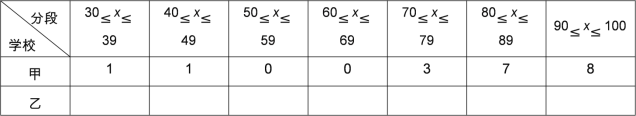
分析數據 :
兩組數據的平均數、中位數、眾數、方差如下表:

a經統計,表格中m的值是 ___________ .
得出結論:
b若甲學校有 400 名初二學生,估計這次考試成績 80 分以上人數為____________ .
c可以推斷出 _______學校學生的數學水平較高,理由為:①__________________;②_________________.(至少從兩個不同的角度說明推斷的合理性)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2014年鄭州市城鎮民營企業就業人數突破20萬,為了解城鎮民營企業員工每月的收入狀況,統計局對全市城鎮企業民營員工2014年月平均收入隨機抽樣調查,將抽樣的數據按“2000元以內”、“2000元~4000元”、“4000元~6000元”和“6000元以上”分為四組,進行整理,分別用A,B,C,D表示,得到下列兩幅不完整的統計圖.
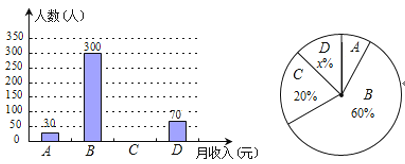
由圖中所給出的信息解答下列問題:
(1)本次抽樣調查的員工有_____人,在扇形統計圖中x的值為_____,表示“月平均收入在2000元以內”的部分所對應扇形的圓心角的度數是_____;
(2)將不完整的條形圖補充完整,并估計我市2013年城鎮民營企業20萬員工中,每月的收入在“2000元~4000元”的約多少人?
(3)統計局根據抽樣數據計算得到,2013年我市城鎮民營企業員工月平均收入為4872元,請你結合上述統計的數據,談一談用平均數反映月收入情況是否合理?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2013年5月31日是第26個“世界無煙日”,校學生會書記小明同學就“戒煙方式”的了解程度對本校九年級學生進行了一次隨機問卷調查,如圖是他采集數據后繪制的兩幅不完整的統計圖(A:了解較多,B:不了解,C:了解一點,D:非常了解).請你根據圖中提供的信息解答以下問題:
(1)在扇形統計圖中的橫線上填寫缺失的數據,并把條形統計圖補充完整.
(2)2013年該初中九年級共有學生400人,按此調查,可以估計2013年該初中九年級學生中對戒煙方式“了解較多”以上的學生約有多少人?
(3)在問卷調查中,選擇“A”的是1名男生,1名女生,選擇“D”的有4人且有2男2女.校學生會要從選擇“A、D”的問卷中,分別抽一名學生參加活動,請你用列表法或樹狀圖求出恰好是一名男生一名女生的概率.
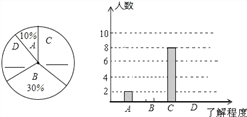
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=mx2+2mx+m-1和直線y=mx+m-1,且m≠0.
(1)求拋物線的頂點坐標;
(2)試說明拋物線與直線有兩個交點;
(3)已知點T(t,0),且-1≤t≤1,過點T作x軸的垂線,與拋物線交于點P,與直線交于點Q,當0<m≤3時,求線段PQ長的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com