
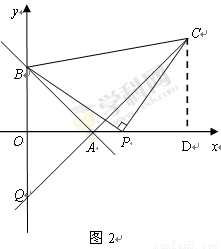
(本題滿分12分)已知,如圖,一次函數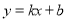 與x軸、y軸分別交于點A和點B,A點坐標為(3,0),∠OAB=45°.
與x軸、y軸分別交于點A和點B,A點坐標為(3,0),∠OAB=45°.
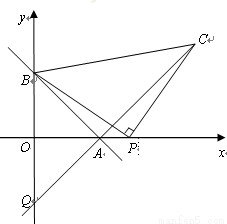
(1)求一次函數的表達式;
(2)點P是x軸正半軸上一點,以P為直角頂點,BP為腰在第一象限內作等腰Rt△BPC,連接CA并延長交y軸于點Q.
①若點P的坐標為(4,0),求點C的坐標,并求出直線AC的函數表達式;
②當P點在x軸正半軸運動時,Q點的位置是否發現變化?若不變,請求出它的坐標;如果變化,請求出它的變化范圍.
(1)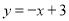 ;(2)①點C(7,4);
;(2)①點C(7,4);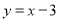 ;②點Q的位置不發生變化,點Q的坐標為(0,-3).
;②點Q的位置不發生變化,點Q的坐標為(0,-3).
【解析】
試題分析:(1)由∠AOB=90°,∠OAB=45°,可得∠OBA=∠OAB=45°,即OA=OB,由A(3,0),可得B(0,3),代入y=kx+b可得出k,b的值,即可得出一次函數的表達式;
(2)①過點C作x軸的垂線,垂足為D,易證△BOP≌△PDC,進而得出點P,C的坐標,把點A,C的坐標代入y=k1x+b1求解即可;
②由△BOP≌△PDC,可得PD=BO,CD=PO,由線段關系進而得出OA=OB,得出AD=CD,由角的關系可得△AOQ是等腰直角三角形,可得出OQ=OA,即可得出點Q的坐標.
試題解析:【解析】
(1)∵∠AOB=90°,∠OAB=45°,
∴∠OBA=∠OAB=45°,
∴OA=OB,
∵A(3,0),
∴B(0,3),
∴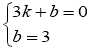 ,解得
,解得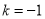 ,
,
∴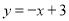 ;
;
(2)①過點C作x軸的垂線,垂足為D,
∵∠BPO+∠CPD=∠PCD+∠CPD=90°,
∴∠BPO=∠PCD,
在△BOP和 △PDC 中,
 ,
,
∴ △BOP≌ △PDC(AAS).
∴PD=BO=3,CD=PO,
∵P(4,0),
∴CD=PO=4, 則OD=3+4=7,
∴ 點C(7,4),
設直線AC的函數關系式為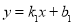 ,
,
則 ,解得
,解得 ,
,
∴直線AC的函數關系式為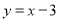 ;
;
②點Q的位置不發生變化.
理由:由①知 △BOP≌ △PDC,
當P點在x軸正半軸運動時,仍有△BOP≌ △PDC,
∴PD=BO,CD=PO,
∴PO+PD=CD+OB,
即OA+AD=OB+CD,
又∵OA=OB,
∴AD=CD,
∴∠CAD=45°,
∴∠CAD=∠QAO=45°,
∴OQ=OA=3,
即點Q的坐標為(0,-3).
考點:待定系數法求一次函數解析式;全等三角形的判定和性質.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源:2014-2015學年北京市房山區九年級上學期期末考試數學試卷(解析版) 題型:解答題
小紅想要測量校園內一座教學樓CD的高度.她先在A處測得樓頂C的仰角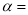 30°,再向樓的方向直行10米到達B處,又測得樓頂C的仰角
30°,再向樓的方向直行10米到達B處,又測得樓頂C的仰角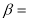 60°,若小紅的目高(眼睛到地面的高度)AE為1.60米,請你幫助她計算出這座教學樓CD的高度(結果精確到0.1米)參考數據:
60°,若小紅的目高(眼睛到地面的高度)AE為1.60米,請你幫助她計算出這座教學樓CD的高度(結果精確到0.1米)參考數據: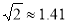 ,
,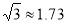 ,
,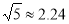

查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省濱海縣七年級上學期期末考試數學試卷(解析版) 題型:選擇題
下列長度的3根小木棒能搭成三角形的是( ).
A.3cm,5 cm,5 cm B.4 cm,5 cm,9 cm
C.4 cm,6 cm,11 cm. D.12 cm,5 cm,5 cm
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省濱海縣八年級上學期期末考試數學試卷(解析版) 題型:解答題
(本題滿分10分)
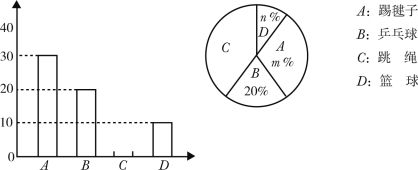
某校為了解“陽光體育”活動的開展情況,從全校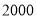 名學生中,隨機抽取部分學生進行問卷調查(每名學生只能填寫一項自己喜歡的活動項目),并將調查結果繪制成如下兩幅不完整的統計圖.
名學生中,隨機抽取部分學生進行問卷調查(每名學生只能填寫一項自己喜歡的活動項目),并將調查結果繪制成如下兩幅不完整的統計圖.
根據以上信息,解答下列問題:
(1)被調查的學生共有 人,并補全條形統計圖;
(2)在扇形統計圖中,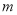 = ,
= ,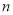 = ,表示區域
= ,表示區域 的圓心角為 °;
的圓心角為 °;
(3)全校學生中喜歡籃球的人數大約有多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com