
隨著“六一”臨近,兒童禮品開始熱銷,某廠每月固定生產甲、乙兩種禮品共100萬件,甲禮品每件成本15元,乙禮品每件成本12元,現甲禮品每件售價22元,乙禮品每件售價18元,且都能全部售出。
(1)若某月銷售收入2000萬元,則該月甲、乙禮品的產量分別是多少?
(2)如果每月投入的總成本不超過1380萬元,應怎樣安排甲、乙禮品的產量,可使所獲得的利潤最大?
(3)該廠在銷售中發現:甲禮品售價每提高1元,銷量會減少4萬件,乙禮品售價不變,不管多少產量都能賣出。在(2)的條件下,為了獲得更大的利潤,該廠決定提高甲禮品的售價,并重新調整甲、乙禮品的生產數量,問:提高甲禮品的售價多少元時可獲得最大利潤,最大利潤為多少萬元?
(1)50萬件,50萬件;(2)甲禮品60萬件,乙禮品40萬件;(3)7元,856萬元
【解析】
試題分析:(1)設生產甲禮品 萬件,乙禮品
萬件,乙禮品 萬件,根據“月銷售收入2000萬元”即可列方程求解;
萬件,根據“月銷售收入2000萬元”即可列方程求解;
(2)設生產甲禮品 萬件,乙禮品
萬件,乙禮品 萬件,所獲得的利潤為
萬件,所獲得的利潤為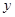 萬元,根據“每月投入的總成本不超過1380萬元”即可列不等式求解;
萬元,根據“每月投入的總成本不超過1380萬元”即可列不等式求解;
(3)設提價甲禮品 元,先根據題意列出y關于a的函數關系式,再根據二次函數的性質求解即可.
元,先根據題意列出y關于a的函數關系式,再根據二次函數的性質求解即可.
(1)設生產甲禮品 萬件,乙禮品
萬件,乙禮品 萬件,由題意得:
萬件,由題意得:
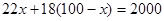
解得: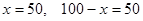
答:甲、乙禮品的產量分別是50萬件,50萬件;
(2)設生產甲禮品 萬件,乙禮品
萬件,乙禮品 萬件,所獲得的利潤為
萬件,所獲得的利潤為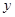 萬元,由題意得
萬元,由題意得
 ,解得
,解得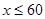
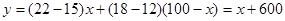
∵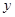 隨
隨 增大而增大,
增大而增大,
∴當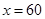 萬件時,y有最大值660萬元。
萬件時,y有最大值660萬元。
答:這時應生產甲禮品60萬件,乙禮品40萬件;
(3)設提價甲禮品 元,由題意得
元,由題意得
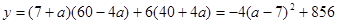
∴當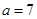 即提價甲禮品7元時,可獲得最大利潤856萬元。
即提價甲禮品7元時,可獲得最大利潤856萬元。
考點:二次函數的應用
點評:此類問題綜合性強,難度較大,在中考中比較常見,一般作為壓軸題,題目比較典型.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2013年浙江省瑞安市初中畢業生學業考試適應性測試數學試卷(帶解析) 題型:解答題
隨著“六一”臨近,兒童禮品開始熱銷,某廠每月固定生產甲、乙兩種禮品共100萬件,甲禮品每件成本15元,乙禮品每件成本12元,現甲禮品每件售價22元,乙禮品每件售價18元,且都能全部售出。
(1)若某月銷售收入2000萬元,則該月甲、乙禮品的產量分別是多少?
(2)如果每月投入的總成本不超過1380萬元,應怎樣安排甲、乙禮品的產量,可使所獲得的利潤最大?
(3)該廠在銷售中發現:甲禮品售價每提高1元,銷量會減少4萬件,乙禮品售價不變,不管多少產量都能賣出。在(2)的條件下,為了獲得更大的利潤,該廠決定提高甲禮品的售價,并重新調整甲、乙禮品的生產數量,問:提高甲禮品的售價多少元時可獲得最大利潤,最大利潤為多少萬元?
查看答案和解析>>
科目:初中數學 來源:2013屆河南省鄭州市第四中學九年級中招模擬數學試卷(帶解析) 題型:解答題
隨著“六一”臨近,兒童禮品開始熱銷,某廠每月固定生產甲、乙兩種禮品共100萬件,甲禮品每件成本15元,乙禮品每件成本12元,現甲禮品每件售價22元,乙禮品每件售價18元,且都能全部售出。
(1)若某月銷售收入2000萬元,則該月甲、乙禮品的產量分別是多少?
(2)如果每月投入的總成本不超過1380萬元,應怎樣安排甲、乙禮品的產量,可使所獲得的利潤最大?
(3)該廠在銷售中發現:甲禮品售價每提高1元,銷量會減少4萬件,乙禮品售價不變,不管多少產量都能賣出。在(2)的條件下,為了獲得更大的利潤,該廠決定提高甲禮品的售價,并重新調整甲、乙禮品的生產數量,問:提高甲禮品的售價多少元時可獲得最大利潤,最大利潤為多少萬元?
查看答案和解析>>
科目:初中數學 來源:2012-2013學年河南省鄭州市九年級中招模擬數學試卷(解析版) 題型:解答題
隨著“六一”臨近,兒童禮品開始熱銷,某廠每月固定生產甲、乙兩種禮品共100萬件,甲禮品每件成本15元,乙禮品每件成本12元,現甲禮品每件售價22元,乙禮品每件售價18元,且都能全部售出。
(1)若某月銷售收入2000萬元,則該月甲、乙禮品的產量分別是多少?
(2)如果每月投入的總成本不超過1380萬元,應怎樣安排甲、乙禮品的產量,可使所獲得的利潤最大?
(3)該廠在銷售中發現:甲禮品售價每提高1元,銷量會減少4萬件,乙禮品售價不變,不管多少產量都能賣出。在(2)的條件下,為了獲得更大的利潤,該廠決定提高甲禮品的售價,并重新調整甲、乙禮品的生產數量,問:提高甲禮品的售價多少元時可獲得最大利潤,最大利潤為多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com