日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 初中數學 > 題目詳情

如圖，AB、CD兩教學樓相距30米，某學生在教室窗口B處測得CD樓樓頂C處的仰角為30°，樓底D處的俯角為45°，則CD的高度為


  1. A.
    （10數學公式+30）米
  2. B.
    （30-數學公式）米
  3. C.
    45米
  4. D.
    5米
A
分析：作BE⊥CD，根據俯仰角的正切值求得AB、CE的長，則CD的高度即可求出．
解答：解：如圖．作BE⊥CD．
由題意得：∠CBE=30°，∠ABD=45°，
則AB==30（米），CE=BE•tan30°=10（米），
∴CD=AB+CE=10+30 （米）．
故選A．
點評：本題考查俯仰角的定義，要求學生能借助俯仰角構造直角三角形并解直角三角形．
練習冊系列答案
相關習題

科目：初中數學 來源： 題型：

數形結合作為一種數學思想方法，數形結合的應用大致又可分為兩種情形：或者借助于數的精確性來闡明形的某些屬性，即“以數解形”；或者借助形的幾何直觀性來闡明數之間的某種關系，即“以形助數”．
如浙教版九上課本第109頁作業題第2題：如圖1，已知在△ABC中，∠ACB=90°，CD⊥AB，D為垂足．易證得兩個結論：（1）AC•BC=AB•CD   （2）AC2=AD•AB
（1）請你用數形結合的“以數解形”思想來解：如圖2，已知在△ABC中（AC＞BC），∠ACB=90°，CD⊥AB，D為垂足，CM平分∠ACB，且BC、AC是方程x2-14x+48=0的兩個根，求AD、MD的長．
（2）請你用數形結合的“以形助數”思想來解：設a、b、c、d都是正數，滿足a：b=c：d，且a最大．求證：a+d＞b+c（提示：不訪設AB=a，CD=d，AC=b，BC=c，構造圖1）
精英家教網

查看答案和解析>>

科目：初中數學 來源： 題型：

（本小題滿分10分）

數形結合作為一種數學思想方法，數形結合的應用大致又可分為兩種情形：或者借助于數的精確性來闡明形的某些屬性，即“以數解形”；或者借助形的幾何直觀性來闡明數之間的某種關系，即 “以形助數”。                                                            

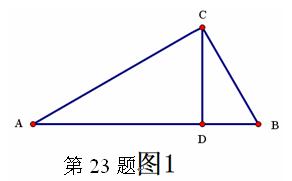
如浙教版九上課本第109頁作業題第2題：如圖1，已知在△ABC中，∠ACB=900，CD⊥AB，D為垂足。易證得兩個結論：(1)AC·BC = AB·CD   (2)AC2= AD·AB

（1）請你用數形結合的“以數解形”思想來解：如圖2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D為垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的兩個根，求AD、MD的長。

（2）請你用數形結合的“以形助數”思想來解： 設a、b、c、d都是正數，滿足a：b=c：d,且a最大。求證：a+d>b+c（提示：不訪設AB=a,CD=d,AC=b,BC=c，構造圖1）

 

查看答案和解析>>

科目：初中數學 來源： 題型：

【改編】（本小題滿分10分）
數形結合作為一種數學思想方法，數形結合的應用大致又可分為兩種情形：或者借助于數的精確性來闡明形的某些屬性，即“以數解形”；或者借助形的幾何直觀性來闡明數之間的某種關系，即“以形助數”。                                                           如浙教版九上課本第109頁作業題第2題：如圖1，已知在△ABC中，∠ACB=900，CD⊥AB，D為垂足。易證得兩個結論：(1)AC·BC = AB·CD   (2)AC2= AD·AB
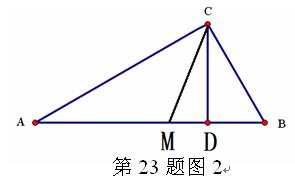
（1）請你用數形結合的“以數解形”思想來解：如圖2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D為垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的兩個根，求AD、MD的長。
（2）請你用數形結合的“以形助數”思想來解：設a、b、c、d都是正數，滿足a：b=c：d,且a最大。求證：a+d>b+c（提示：不訪設AB=a,CD=d,AC=b,BC=c，構造圖1）

查看答案和解析>>

科目：初中數學 來源：2011年南京市溧水縣中考數學一模試卷 題型：解答題

【改編】（本小題滿分10分）
數形結合作為一種數學思想方法，數形結合的應用大致又可分為兩種情形：或者借助于數的精確性來闡明形的某些屬性，即“以數解形”；或者借助形的幾何直觀性來闡明數之間的某種關系，即“以形助數”。                                                           如浙教版九上課本第109頁作業題第2題：如圖1，已知在△ABC中，∠ACB=900，CD⊥AB，D為垂足。易證得兩個結論：(1)AC·BC = AB·CD   (2)AC2= AD·AB
（1）請你用數形結合的“以數解形”思想來解：如圖2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D為垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的兩個根，求AD、MD的長。
（2）請你用數形結合的“以形助數”思想來解：設a、b、c、d都是正數，滿足a：b=c：d,且a最大。求證：a+d>b+c（提示：不訪設AB=a,CD=d,AC=b,BC=c，構造圖1）

查看答案和解析>>

科目：初中數學 來源：2011學年河北省考模擬考試數學卷 題型：選擇題

（本小題滿分10分）

數形結合作為一種數學思想方法，數形結合的應用大致又可分為兩種情形：或者借助于數的精確性來闡明形的某些屬性，即 “以數解形”；或者借助形的幾何直觀性來闡明數之間的某種關系，即 “以形助數”。                                                            

如浙教版九上課本第109頁作業題第2題：如圖1，已知在△ABC中，∠ACB=900，CD⊥AB，D為垂足。易證得兩個結論：(1)AC·BC = AB·CD   (2)AC2= AD·AB

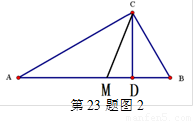
（1）請你用數形結合的“以數解形”思想來解：如圖2，已知在△ABC中（AC>BC），∠ACB=900，CD⊥AB，D為垂足， CM平分∠ACB,且BC、AC是方程x2-14x+48=0的兩個根，求AD、MD的長。

（2）請你用數形結合的“以形助數”思想來解： 設a、b、c、d都是正數，滿足a：b=c：d,且a最大。求證：a+d>b+c（提示：不訪設AB=a,CD=d,AC=b,BC=c，構造圖1）

 

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 久久久久久久久久久久久久久 | 日韩av一区二区三区在线 | 欧美日韩三级 | 亚洲欧美国产另类 | 人人艹人人 | 在线一区观看 | 久久夜色精品国产 | 国产欧美一区在线 | 在线欧美色 | 久久污 | 欧美电影一区二区 | 亚洲一区二区三区四区五区午夜 | 久久国产精品99久久久久久老狼 | 在线观看成人高清 | 综合在线一区 | 欧美国产日韩在线观看 | 一本岛在线视频 | 91精品电影 | 中文字幕一区二区三区四区 | 亚洲一区二区在线电影 | 青青草91视频 | 国产欧美一区二区精品婷 | 日韩欧美一区二区视频 | 欧美韩一区二区 | 国产一区二区 | 欧美一区二区久久久 | 日本成人一区二区三区 | 精品久久久久国产免费 | av手机在线播放 | 免费黄色在线 | 欧美日韩黄色一区二区 | 亚洲午夜精品 | 超碰激情 | 精品国产乱码久久久久久88av | 久久国产精彩视频 | 一区二区免费 | 韩国精品一区二区 | 日日操视频 | 麻豆91在线观看 | 欧美一区二区黄色片 | 亚洲日韩中文字幕天堂不卡 |