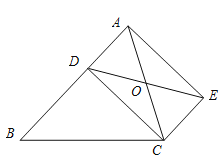
【題目】如圖，已知D是△ABC的邊AB上一點，CE∥AB，DE交AC于點O，且OA=OC，猜想線段CD與線段AE的大小關系和位置關系，并加以證明．
期末沖刺100分創新金卷完全試卷系列答案科目：初中數學 來源： 題型：
【題目】若一個整數能表示成a2+b2（a、b是正整數）的形式，則稱這個數為“豐利數”．例如，2是“豐利數”，因為2=12+12，再如，M=x2+2xy+2y2=（x+y）2+y2（x+y，y是正整數），所以M也是“豐利數”．
（1）請你寫一個最小的三位“豐利數”是 ，并判斷20 “豐利數”．（填是或不是）；
（2）已知S=x2+y2+2x﹣6y+k（x、y是整數，k是常數），要使S為“豐利數”，試求出符合條件的一個k值（10≤k＜200），并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料：
學習了三角形全等的判定方法（即“SAS”“ASA”“AAS”“SSS”）和直角三角形全等的判定方法（即“HL”）后，小聰繼續對“兩個三角形滿足兩邊和其中一邊的對角對應相等”的情形進行研究
小聰將命題用符號語言表示為：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E．
小聰的探究方法是對∠B分為“直角、鈍角、銳角”三種情況進行探究．
第一種情況：當∠B 是直角時，如圖1，△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E=90°，根據“HL”定理，可以知道Rt△ABC≌Rt△DEF．
第二種情況：當∠B 是銳角時，如圖2，BC=EF，∠B=∠E＜90°，在射線EM上有點D，使DF=AC，畫出符合條件的點D，則△ABC和△DEF的關系是 ；
A．全等 B．不全等 C．不一定全等
第三種情況：當∠B是鈍角時，如圖3，在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E＞90°．過點C作AB邊的垂線交AB延長線于點M；同理過點F作DE邊的垂線交DE延長線于N，根據“ASA”，可以知道△CBM≌△FEN，請補全圖形，進而證出△ABC≌△DEF．
查看答案和解析>>
科目：初中數學 來源： 題型：
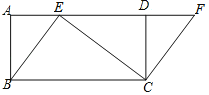
【題目】如圖，四邊形ABCD是矩形，點E在AD邊上，點F在AD的延長線上，且BE=CF．
（1）求證：四邊形EBCF是平行四邊形．
（2）若∠BEC=90°，∠ABE=30°，AB=
，求ED的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】ABCD中，E是CD邊上一點，
（1）將△ADE繞點A按順時針方向旋轉，使AD、AB重合，得到△ABF，如圖1所示．觀察可知：與DE相等的線段是 ，∠AFB=∠
（2）如圖2，正方形ABCD中，P、Q分別是BC、CD邊上的點，且∠PAQ=45°，試通過旋轉的方式說明：DQ+BP=PQ；
（3）在（2）題中，連接BD分別交AP、AQ于M、N，你還能用旋轉的思想說明BM2+DN2=MN2嗎？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在△ABC中，AB=AC，D為邊BC上一點，以AB，BD為鄰邊作平行四邊形ABDE，連接AD，EC．
（1）求證：△ADC≌△ECD；
（2）當點D在什么位置時，四邊形ADCE是矩形，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列條件：①∠A＝∠B＝∠C；②∠A∶∠B∶∠C＝1∶2∶3；③∠A＝90°＋∠B；④∠A＝∠B＝
∠C，能確定△ABC是直角三角形的條件有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我市某綠色無公害蔬菜基地有甲、乙兩種植戶，他們們種植了A、B兩類蔬菜，兩種植戶種植的兩類蔬菜的種植面積與總收入如下表：
種植戶 | 種植A類蔬菜面積（單位：畝） | 種植B類蔬菜面積（單位：畝） | 總收入（單位：元） |
甲 | 1 | 3 | 13500 |
乙 | 2 | 2 | 13000 |
說明：不同種植戶種植的同類蔬菜每畝平均收入相等
（1）求A、B兩類蔬菜每畝平均收入各是多少元？
（2）今年甲、乙兩種植戶聯合種植，計劃合租50畝地用來種植A、B兩類蔬菜，為了使總收入不低于16400元，問聯合種植最多可以種植A類蔬菜多少畝？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
