
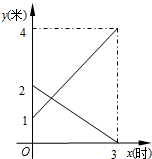 的深度y(米)與注水時間x(時)之間的函數圖象如圖所示,結合圖象回答下列問題:
的深度y(米)與注水時間x(時)之間的函數圖象如圖所示,結合圖象回答下列問題: ,b=2代入函數關系式y=kx+b中得,
,b=2代入函數關系式y=kx+b中得, x+2
x+2 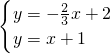
 .
. 小時后,甲、乙兩個蓄水池水的深度相同;
小時后,甲、乙兩個蓄水池水的深度相同; x+2)=S2(x+1),
x+2)=S2(x+1),

 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
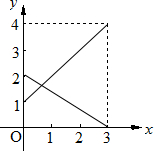 甲、乙兩個蓄水池中水的深度y(米)與注水時間x(時)之間的函數圖象如圖所示,結合圖象回答下列問題:
甲、乙兩個蓄水池中水的深度y(米)與注水時間x(時)之間的函數圖象如圖所示,結合圖象回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:
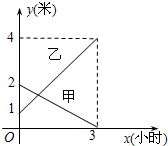 某企業有甲、乙兩個長方體的蓄水池,將甲池中的水以一定的速度注入乙池,甲、乙兩個蓄水池中水的深度y(米)與注水時間x(時)之間的函數圖象如圖所示,結合圖象回答下列問題:
某企業有甲、乙兩個長方體的蓄水池,將甲池中的水以一定的速度注入乙池,甲、乙兩個蓄水池中水的深度y(米)與注水時間x(時)之間的函數圖象如圖所示,結合圖象回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:
 的深度y(米)與注水時間x(時)之間的函數圖象如圖所示,結合圖象回答下列問題:
的深度y(米)與注水時間x(時)之間的函數圖象如圖所示,結合圖象回答下列問題:查看答案和解析>>
科目:初中數學 來源:2011年湖北省鄂州市石山中學中考數學模擬試卷(三)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2005年全國中考數學試題匯編《一次函數》(04)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com