
【題目】在平面直角坐標系中,![]() 為坐標原點,過二次函數
為坐標原點,過二次函數![]() 圖象上的點
圖象上的點![]() ,作
,作![]() 軸的垂線交
軸的垂線交![]() 軸于點
軸于點![]() .
.
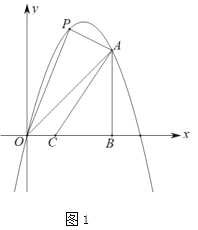
(1)如圖1,![]() 為線段
為線段![]() 上方拋物線上的一點,在
上方拋物線上的一點,在![]() 軸上取點
軸上取點![]() ,點
,點![]() 、
、![]() 為
為![]() 軸上的兩個動點,點
軸上的兩個動點,點![]() 在點
在點![]() 的上方且
的上方且![]() 連接
連接![]() ,當四邊形
,當四邊形![]() 的面積最大時,求
的面積最大時,求![]() 的最小值.
的最小值.
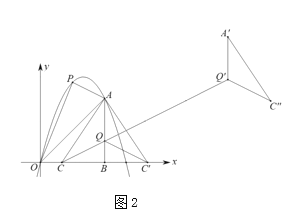
(2)如圖2,點![]() 在線段
在線段![]() 上,連接
上,連接![]() ,將
,將![]() 沿直線
沿直線![]() 翻折,
翻折,![]() 點的對應點為
點的對應點為![]() ,將
,將![]() 沿射線
沿射線![]() 平移
平移![]() 個單位得
個單位得![]() ,在拋物線上取一點
,在拋物線上取一點![]() ,使得以
,使得以![]() 為頂點的三角形是等腰三角形,求
為頂點的三角形是等腰三角形,求![]() 點的坐標.
點的坐標.
【答案】(1)![]() (2)(7,3),(
(2)(7,3),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(13,6),(10,
),(13,6),(10,![]() ).
).
【解析】
(1)把四邊形PACO沿OA分成△OAP與△OAC,由于△OAC三邊確定,面積為定值,故△OAP面積最大時四邊形面積也最大.過點P作x軸垂線交OA于D,設點P橫坐標為t,則能用t表示PD的長,進而得到△OAP關于t的二次函數關系式,用公式法可求得t=![]() 時△OAP面積最大,即求得此時點P坐標.把點P向下平移1個單位得P',易證四邊形MNP'P是平行四邊形,所以PM=P'N.過點O作經過第二、四象限的直線l,并使直線l與x軸夾角為60°,過點N作NG⊥直線l于點G,則由30°角所對直角邊等于斜邊一半可知NG=
時△OAP面積最大,即求得此時點P坐標.把點P向下平移1個單位得P',易證四邊形MNP'P是平行四邊形,所以PM=P'N.過點O作經過第二、四象限的直線l,并使直線l與x軸夾角為60°,過點N作NG⊥直線l于點G,則由30°角所對直角邊等于斜邊一半可知NG=![]() NO.所以PM+MN+
NO.所以PM+MN+![]() NO可轉化為P'N+NG+1,易得當點P'、N、G在同一直線上最小.把PD延長交直線l于點F,構造特殊Rt△P'FG和Rt△OEF,利用點P坐標和30°、60°的三角函數即可求得P'G的長.
NO可轉化為P'N+NG+1,易得當點P'、N、G在同一直線上最小.把PD延長交直線l于點F,構造特殊Rt△P'FG和Rt△OEF,利用點P坐標和30°、60°的三角函數即可求得P'G的長.
(2)由點B、C、Q的坐標求CQ的長和點C'坐標;過點Q'作x軸的垂線段Q'H,易證△CBQ∽△CHQ',故有![]() ,求得CH、HQ'的長即求得點Q'坐標,進而得到向右向上平移的距離,求得點A'、C'的坐標.求直線CQ解析式,設CQ上的點M橫坐標為m,用兩點間距離公式可得用m表示A'M和C'M的長.因為△A'MC'是等腰三角形,分三種情況討論,得到關于m的方程,求解即求得相應的m的值,進而得點M坐標.
,求得CH、HQ'的長即求得點Q'坐標,進而得到向右向上平移的距離,求得點A'、C'的坐標.求直線CQ解析式,設CQ上的點M橫坐標為m,用兩點間距離公式可得用m表示A'M和C'M的長.因為△A'MC'是等腰三角形,分三種情況討論,得到關于m的方程,求解即求得相應的m的值,進而得點M坐標.
解:(1)如圖1,過點O作直線l,使直線l經過第二、四象限且與x軸夾角為60°;
過點P作PF⊥x軸于點E,交OA于點D,交直線l于點F;在PF上截取PP'=1;過點N作NG⊥直線l于點G
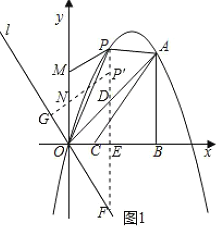
∵A(3,3),AB⊥x軸于點B
∴直線OA解析式為y=x,OB=AB=3
∵C(1,0)
∴S△AOC=![]() OCAB=
OCAB=![]() ×1×3=
×1×3=![]() ,是定值
,是定值
設P(t,t2+4t)(0<t<3)
∴D(t,t)
∴PD=t2+4tt=t2+3t
∴S△OAP=S△OPD+S△APD=![]() PDOE+
PDOE+![]() PDBE=
PDBE=![]() PDOB=
PDOB=![]() (t23t)
(t23t)
∴t=![]() =
=![]() 時,S△OAP最大
時,S△OAP最大
此時,S四邊形PACO=S△AOC+S△OAP最大
yP=(![]() )2+3×
)2+3×![]() =
=![]()
∴P(![]() ,
,![]() )
)
∴P'E=PEPP'=![]() 1=
1=![]() ,即P'(
,即P'(![]() ,
,![]() )
)
∵點M、N在y軸上且MN=1
∴PP'=MN,PP'∥MN
∴四邊形MNP'P是平行四邊形
∴PM=P'N
∵∠NGO=90°,∠NOG=90°60°=30°
∴Rt△ONG中,NG=![]() NO
NO
∴PM+MN+![]() NO=P'N+NG+1
NO=P'N+NG+1
∴當點P'、N、G在同一直線上,即P'G⊥直線l時,PM+MN+![]() NO=P'G+1最小
NO=P'G+1最小
∵OE=![]() ,∠EOF=60°,∠OEF=90°
,∠EOF=60°,∠OEF=90°
∴Rt△OEF中,∠OFE=30°,tan∠EOF=![]() =
=![]()
∴EF=![]() OE=
OE=![]()
∴P'F=P'E+EF=![]() +
+![]()
∴Rt△P'GF中,P'G=![]() P'F=
P'F=![]()
∴P'G+1=![]() +1=
+1=![]()
∴PM+MN+![]() NO的最小值為
NO的最小值為![]()
(2)延長A'Q'交x軸于點H
∵C(1,0),Q(3,1),QB⊥x軸于點B
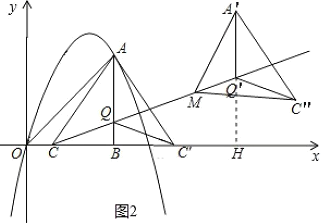
∴CB=2,BQ=1
∴CQ=![]() =
=![]()
∵△AQC沿直線AB翻折得△AQC'
∴B(3,0)是CC'的中點
∴C'(5,0)
∵平移距離QQ'=3![]()
∴CQ'=CQ+QQ'=4![]()
∵QB∥Q'H
∴△CBQ∽△CHQ'
∴![]()
∴CH=4CB=8,yQ'=HQ'=4BQ=4
∴xQ'=OC+CH=1+8=9
∴Q'(9,4)
∴點Q(3,1)向右平移6個單位,向上平移3個單位得到點Q'(9,4)
∴A'(9,6),C'(11,3)
∴A'C'=![]()
設直線CQ解析式為y=kx+b
∴![]()
解得: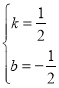
∴直線CQ:y=![]() x
x![]()
設射線CQ上的點M(m,![]() m
m![]() )(m>1)
)(m>1)
∴A'M2=(9m)2+(6![]() m+
m+![]() )2=(9m)2+(
)2=(9m)2+(![]() )2
)2
C'M2=(11m)2+(3![]() m+
m+![]() )2=(11m)2+(
)2=(11m)2+(![]() )2
)2
∵△A'MC'是等腰三角形
故①若A'M=A'C',則(9m)2+(![]() )2=13
)2=13
解得:m1=7,m2=![]()
∴M(7,3)或(![]() ,
,![]() )
)
②若C'M=A'C',則(11m)2+(![]() )2=13
)2=13
解得:m1=![]() ,m2=13
,m2=13
∴M(![]() ,
,![]() )或(13,6)
)或(13,6)
③若A'M=C'M,則(9m)2+(![]() )2=(11m)2+(
)2=(11m)2+(![]() )2
)2
解得:m=10
∴M(10,![]() )
)
綜上所述,點M坐標為(7,3),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(13,6),(10,
),(13,6),(10,![]() ).
).


科目:初中數學 來源: 題型:
【題目】春節期間,甲、乙兩家水果店以同樣的價格銷售同一種水果,它們的優惠方案分別為:甲水果店,一次性購水果超過![]() 元,超過部分打七折;乙水果店,一次性購水果超過
元,超過部分打七折;乙水果店,一次性購水果超過![]() 元,超過部分打五折,設水果售價為
元,超過部分打五折,設水果售價為![]() (單位:元)
(單位:元)![]() ,在甲.乙兩家水果店購水果應付金額為
,在甲.乙兩家水果店購水果應付金額為![]() (單位:元),
(單位:元),![]() (單位:元),
(單位:元),![]() 與
與![]() 之間的函數關系如圖所示.
之間的函數關系如圖所示.
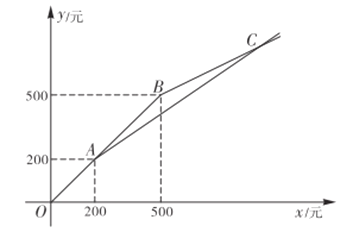
(1)求甲水果店購水果應付金額![]() 與水果售價
與水果售價![]() 之間的函數關系式;
之間的函數關系式;
(2)求交點![]() 的坐標;
的坐標;
(3)根據圖象,請直接寫出春節期間選擇哪家水果店購水果更優惠.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知水銀體溫計的讀數y(℃)與水銀柱的長度x(cm)之間是一次函數關系.現有一支水銀體溫計,其部分刻度線不清晰(如圖),表中記錄的是該體溫計部分清晰刻度線及其對應水銀柱的長度.
水銀柱的長度x(cm) | 4.2 | … | 8.2 | 9.8 |
體溫計的讀數y(℃) | 35.0 | … | 40.0 | 42.0 |
(1)求y關于x的函數關系式(不需要寫出函數的定義域)
(2)用該體溫計測體溫時,水銀柱的長度為6.6cm,求此時體溫計的讀數.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
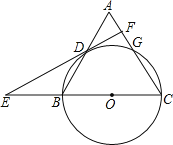
【題目】如圖,在三角形ABC中,AB=6,AC=BC=5,以BC為直徑作⊙O交AB于點D,交AC于點G,直線DF是⊙O的切線,D為切點,交CB的延長線于點E.
(1)求證:DF⊥AC;
(2)求tan∠E的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
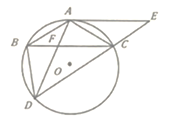
【題目】如圖,在平行四邊形ABCD中,連接AC,做△ABC的外接圓⊙O,延長EC交⊙O于點D,連接BD、AD,BC與AD交于點F分,∠ABC=∠ADB。
(1)求證:AE是⊙O的切線;
(2)若AE=12,CD=10,求⊙O的半徑。
查看答案和解析>>
科目:初中數學 來源: 題型:
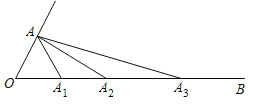
【題目】如圖,已知![]() ,點
,點![]() 繞點
繞點![]() 順時針旋轉后的對應點
順時針旋轉后的對應點![]() 落在射線
落在射線![]() 上,點
上,點![]() 繞點
繞點![]() 順時針旋轉后的對應點
順時針旋轉后的對應點![]() 落在射線
落在射線![]() 上,點
上,點![]() 繞點
繞點![]() 順時針旋轉后的對應點
順時針旋轉后的對應點![]() 落在射線
落在射線![]() 上….連接
上….連接![]() ,依此做法,則
,依此做法,則![]() =________,
=________,![]() =________(用含
=________(用含![]() 的代數式表示,
的代數式表示,![]() 為正整數)
為正整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】外線投資是籃球隊常規訓練的重要項目之一,下列圖表中數據是甲乙丙三從每從十次投籃測試的成績,測試規則為連續投籃十個球為一次,投進籃筐一個球記為1分.
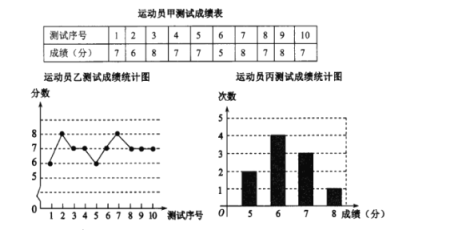
(1)寫出運動員乙測試成績的眾數和中位數;
(2)在他們三從中選擇一位投籃成績優秀且較為穩定的選手作為中鋒,你認為選誰更合適?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象過點
的圖象過點![]() 且與直線
且與直線![]() 相交于
相交于![]() 、
、![]() 兩點,點
兩點,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸上.
軸上.
![]() 求二次函數的解析式.
求二次函數的解析式.
![]() 如果
如果![]() 是線段
是線段![]() 上的動點,
上的動點,![]() 為坐標原點,試求
為坐標原點,試求![]() 的面積
的面積![]() 與
與![]() 之間的函數關系式,并求出自變量的取值范圍.
之間的函數關系式,并求出自變量的取值范圍.
![]() 是否存在這樣的點
是否存在這樣的點![]() ,使
,使![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com