Question

如圖：已知E、F分別是□ABCD的邊BC、AD上的點，且BE=DF．

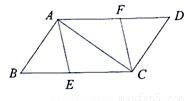
（1）求證：四邊形AECF是平行四邊形；

（2）若BC＝10，∠BAC＝90°，且四邊形AECF是菱形，求BE的長 ．

 

Answer 1

【答案】

（1）證明見解析；（2）5.

【解析】

試題分析：（1）首先由已知證明AF∥EC，BE=DF，推出四邊形AECF是平行四邊形.（2）由已知先證明AE=BE，即BE=AE=CE，從而求出BE的長.

試題解析：（1）∵四邊形ABCD是平行四邊形，∴AD∥BC，AD＝BC. ∴AF∥EC.

∵BE＝DF，∴AF＝EC. ∴四邊形AECF是平行四邊形.

（2）如圖，∵四邊形AECF是菱形，∴AE＝EC。∴∠1＝∠2.

∵∠3＝90°－∠2，∠4＝90°－∠1，∴∠3＝∠4.

∴AE＝BE.

∴BE＝AE＝CE＝BC＝5.

考點：1.平行四邊形的判定和性質；2.菱形的性質；3.等腰三角形的性質；4.三角形內角和定理.