
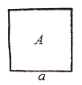
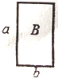
【題目】如圖(1),有![]() 、
、![]() 、
、![]() 三種不同型號的卡片若干張,其中
三種不同型號的卡片若干張,其中![]() 型是邊長為
型是邊長為![]()
![]() 的正方形,
的正方形,![]() 型是長為
型是長為![]() 、寬為
、寬為![]() 的長方形,
的長方形,![]() 型是邊長為
型是邊長為![]() 的正方形.
的正方形.

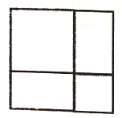
圖(1) 圖(2)
(1)若用![]() 型卡片
型卡片![]() 張,
張,![]() 型卡片
型卡片![]() 張,
張,![]() 型卡片
型卡片![]() 張拼成了一個正方形(如圖(2)),此正方形的邊長為_______,根據該圖形請寫出一條屬于因式分解的等式:_________;
張拼成了一個正方形(如圖(2)),此正方形的邊長為_______,根據該圖形請寫出一條屬于因式分解的等式:_________;
(2)若要拼一個長為![]() ,寬為
,寬為![]() 的長方形,設需要
的長方形,設需要![]() 類卡片
類卡片![]() 張,
張,![]() 類卡片
類卡片![]() 張,
張,![]() 類卡片
類卡片![]() 張,則
張,則![]() _______;
_______;
(3)現有![]() 型卡片
型卡片![]() 張,
張,![]() 型卡片
型卡片![]() 張,
張,![]() 型卡片
型卡片![]() 張,從這
張,從這![]() 張卡片中拿掉兩張卡片,余下的卡片全用上,你能拼出一個長方形或正方形嗎?有幾種拼法?請你通過運算說明理由.
張卡片中拿掉兩張卡片,余下的卡片全用上,你能拼出一個長方形或正方形嗎?有幾種拼法?請你通過運算說明理由.
【答案】(1)a+b,a2+2ab+b2=(a+b)2;(2)9;(3)(3)四種拼法,理由見解析.
【解析】
(1)由圖可得可得正方形的邊長為a+b,由圖(2)可得因式分解的等式![]() ;
;
(2)因為![]() ,所以需要用
,所以需要用![]() 類卡片2張,
類卡片2張,![]() 類卡片5張,
類卡片5張,![]() 類卡片2張,即可求
類卡片2張,即可求![]() 、
、![]() 、
、![]() 對應的值;
對應的值;
(3)分類討論:第一種:![]() 型卡片拿掉1張,
型卡片拿掉1張,![]() 型卡片拿掉1張,則能拼出一個長方形,即長方形的長為
型卡片拿掉1張,則能拼出一個長方形,即長方形的長為![]() ,寬為
,寬為![]() ;第二種:
;第二種:![]() 型卡片拿掉1張,
型卡片拿掉1張,![]() 型卡片拿掉1張,則能拼出一個長方形,即長方形的長為
型卡片拿掉1張,則能拼出一個長方形,即長方形的長為![]() ,寬為
,寬為![]() ,此種情況有兩種;第三種:
,此種情況有兩種;第三種:![]() 型卡片拿掉2張,則能拼出一個正方形方形,即正方形邊長為
型卡片拿掉2張,則能拼出一個正方形方形,即正方形邊長為![]() .
.
(1)由圖(1)和圖(2)可得正方形的邊長為:a+b,
由圖(2)可得因式分解的等式a2+2ab+b2=(a+b)2.
故答案為a+b,a2+2ab+b2=(a+b)2;
(2)∵(2a+b)(a+2b)=2a2+5ab+2b2,
∴需要用A類卡片2張,B類卡片5張,C類卡片2張,
∴x+y+z=2+5+2=9;
故答案為9;
(3)四種拼法:理由如下:
第一種:A型卡片拿掉1張,B型卡片拿掉1張,則能拼出一個長方形,即長方形的長為5a+11b,寬為b,
∴![]()
第二種:A型卡片拿掉1張,C型卡片拿掉1張,則能拼出一個長方形,即長方形的長為3a+5b,寬為2b,
∴![]() ;
;
或者長為6a+10b,寬為b,
![]() ,此種情況共2種拼法;
,此種情況共2種拼法;
第三種:C型卡片拿掉2張,則能拼出一個正方形方形,即正方形邊長為a+3b,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
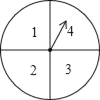
【題目】小王和小張利用如圖所示的轉盤做游戲,轉盤的盤面被分為面積相等的4個扇形區域,且分別標有數字1,2,3,4.游戲規則如下:兩人各轉動轉盤一次,分別記錄指針停止時所對應的數字,如兩次的數字都是奇數,則小王勝;如兩次的數字都是偶數,則小張勝;如兩次的數字是奇偶,則為平局.解答下列問題:
(1)小王轉動轉盤,當轉盤指針停止,對應盤面數字為奇數的概率是多少?
(2)該游戲是否公平?請用列表或畫樹狀圖的方法說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形ABCD,點F是射線DC上一動點(不與C,D重合).連接AF并延長交直線BC于點E,交BD于H,連接CH,過點C作CG⊥HC交AE于點G.
(1)若點F在邊CD上,如圖1.
①證明:∠DAH=∠DCH;
②猜想:△GFC的形狀并說明理由.
(2)取DF中點M,連接MG.若MG=2.5,正方形邊長為4,求BE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場將進貨價為30元的臺燈以40元的價格售出,平均每月能售出600個,經調查表明,這種臺燈的售價每上漲1元,其銷量就減少10個,市場規定此臺燈售價不得超過60元,為了實現銷售這種臺燈平均每月10000元的銷售利潤,售價應定為多少元?這時售出臺燈多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖顯示了用計算機模擬隨機投擲一枚圖釘的某次實驗的結果.下面有三個推斷:①某次實驗投擲次數是500,計算機記錄“釘尖向上”的次數是308,則該次試驗“釘尖向上”的頻率是0.616;②隨著實驗次數的增加,“釘尖向上”的頻率總在0.618附近擺動,顯示出一定的穩定性,可以估計“釘尖向上”的概率是0.618;③若再次用計算機模擬實驗,則當投擲次數為1000時,“釘尖向上”的概率一定是0.620.其中合理的是( )

A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某網店銷售甲、乙兩種羽毛球,已知甲種羽毛球每筒的售價比乙種羽毛球每筒的售價多15元,健民體育活動中心從該網店購買了2筒甲種羽毛球和3筒乙種羽毛球,共花費255元.
(1)該網店甲、乙兩種羽毛球每筒的售價各是多少元?
(2)根據健民體育活動中心消費者的需求量,活動中心決定用不超過2550元錢購進甲、乙兩種羽毛球共50筒,那么最多可以購進多少筒甲種羽毛球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】盤錦市雙臺子區為了了解2016年初中畢業生畢業后的去向,對部分初三學生進行了抽樣調查,就初三學生的四種去向:A.讀普通高中;B.讀職業高中C.直接進入社會就業;D.其它;進行數據統計,并繪制了兩幅不完整的統計圖(a)、(b).請問:
(1)該縣共調查了______名初中畢業生;
(2)將兩幅統計圖中不完整的部分補充完整;
(3)若雙臺子區2016年初三畢業生共有4500人,請估計雙臺子區今年的初三畢業生中讀普通高中的學生人數.
(4)老師想從甲、乙、丙、丁4位同學中隨機選擇兩位同學了解他們畢業后的去向情況,請用樹狀圖或列表法求選中甲同學的概率。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2﹣(2m+1)x+m2+![]() =0有兩個不相等的實數根.
=0有兩個不相等的實數根.
(1)求m的取值范圍;
(2)若m為(1)中符合條件的最小正整數,設此時對應的一元二次方程的兩個實數根分別為α,β,求代數式![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com