
【題目】點(3,﹣2)先向右平移2個單位,再向上平移4個單位,所得的點關于以y軸為對稱點的坐標為__.
科目:初中數學 來源: 題型:
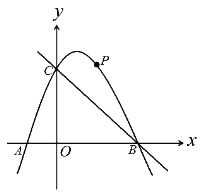
【題目】如圖,在平面直角坐標系中,二次函數![]() 的圖象與x軸交于A、B兩點, 與y軸交于C(0,3),A點在原點的左側,B點的坐標為(3,0))。點P是拋物線上一個動點,且在直線BC的上方.
的圖象與x軸交于A、B兩點, 與y軸交于C(0,3),A點在原點的左側,B點的坐標為(3,0))。點P是拋物線上一個動點,且在直線BC的上方.
(1)求這個二次函數的表達式.
(2)連接PO、PC,并把△POC沿CO翻折,得到四邊形![]() ,那么是否存在點P,使四邊形
,那么是否存在點P,使四邊形![]() 為菱形?若存在,請求出此時點P的坐標;若不存在,請說明理由.
為菱形?若存在,請求出此時點P的坐標;若不存在,請說明理由.
(3)當點P運動到什么位置時,使△BPC的面積最大,求出點P的坐標和△BPC的面積最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:n=p×q(p,q是正整數,且p≤q),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p×q是n的最佳分解.并規定:F(n)= ![]() .例如12可以分解成1×12,2×6或3×4,因為12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因為12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)= ![]() .
.
(1)如果一個正整數a是另外一個正整數b的平方,我們稱正整數a是完全平方數.則對任意一個完全平方數m,F(m)=;
(2)如果一個兩位正整數t,t=10x+y(1≤x≤y≤9,x,y為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為18,那么我們稱這個數t為“吉祥數”,求所有“吉祥數”中F(t)的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】周末,小芳騎自行車從家出發到野外郊游,從家出發0.5小時到達甲地,游玩一段時間后按原速前往乙地,小芳離家1小時20分鐘后,媽媽駕車沿相同路線前往乙地,行駛10分鐘時,恰好經過甲地,如圖是她們距乙地的路程y(km)與小芳離家時間x(h)的函數圖象. 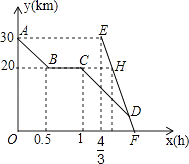
(1)小芳騎車的速度為km/h,H點坐標 .
(2)小芳從家出發多少小時后被媽媽追上?此時距家的路程多遠?
(3)相遇后,媽媽載上小芳和自行車同時到達乙地(彼此交流時間忽略不計),求小芳比預計時間早幾分鐘到達乙地?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若x0是方程ax2+2x+c=0(a≠0)的一個根,設M=1﹣ac,N=(ax0+1)2 , 則M與N的大小關系正確的為( )
A.M>N
B.M=N
C.M<N
D.不確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題:①無理數都是無限小數;② ![]() 的平方根是±4;③等腰三角形的對稱軸是它頂角的平分線;④三角形三邊垂直平分線的交點一定在這個三角形的內部,正確的有( )
的平方根是±4;③等腰三角形的對稱軸是它頂角的平分線;④三角形三邊垂直平分線的交點一定在這個三角形的內部,正確的有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com