
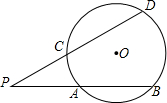
 圓心角度數的一半.類似地,我們定義:頂點在圓外,并且兩邊都和圓相交的角叫做圓外角.
圓心角度數的一半.類似地,我們定義:頂點在圓外,并且兩邊都和圓相交的角叫做圓外角.科目:初中數學 來源: 題型:
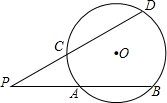 圓心角度數的一半.類似地,我們定義:頂點在圓外,并且兩邊都和圓相交的角叫做圓外角.
圓心角度數的一半.類似地,我們定義:頂點在圓外,并且兩邊都和圓相交的角叫做圓外角.查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
 |
| LN |
 |
| LN |
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
| 1 |
| 2 |
 |
| PQ |
 |
| RT |
 |
| PQ |
 |
| RT |
查看答案和解析>>
科目:初中數學 來源: 題型:
情境一
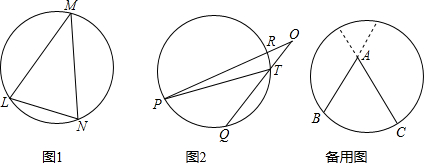
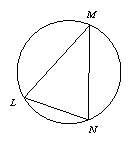
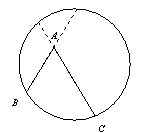
我們知道:頂點在圓上,并且兩邊都和圓相交的角叫做圓周角.我們還知道:①圓心角的度數等于與它所對的弧的度數,②同弧所對的圓周角相等,都等于該弧所對的圓心角的一半.由此,小明得到一個正確的結論:圓周角的度數等于它所對的弧的度數的一半.如圖1,∠LMN=![]()
![]() .
.
問題1 填空:如圖1,如果![]() 的度數是80,那么∠LMN的度數是______.
的度數是80,那么∠LMN的度數是______.
 圖
圖
1
情境二
小明把頂點在圓外,并且兩邊都和圓相交的角叫圓外角,并繼續探索.
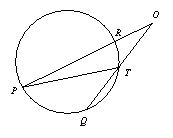
如圖2,∵∠PTQ是△OPT的一個外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ -∠P.
∵圓周角的度數等于它所對的弧的度數的一半(已在情境一中
證明),
∴∠PTQ=![]()
![]() ,∠P=
,∠P=![]()
![]() .
.
∴∠O=∠PTQ -∠P=![]()
![]() -
-![]()
![]() =
=![]() (
(![]() -
-![]() ).
).
經歷了上述探索、證明過程,小明發現了“圓外角的度數等于它所夾的較大弧的度數減去較小弧的度數所得差的一半”這個正確結論.
問題2 填空:如圖2,如果![]() =80°,
=80°,![]() =20°,那么∠O=______°.
=20°,那么∠O=______°.
問題3 類比情境二的內容,請你就角的頂點在圓內的情況進行探索.寫出你的發現,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源:2012年江蘇省南京市聯合體中考數學二模試卷(解析版) 題型:解答題

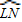 .
.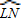 的度數是80,那么∠LMN的度數是______.
的度數是80,那么∠LMN的度數是______.
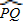 ,∠P=
,∠P=
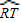 .
.
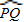 -
-
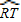 =
= (
(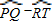 ).
).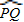 =80°,
=80°,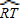 =20°,那么∠O=______°.
=20°,那么∠O=______°.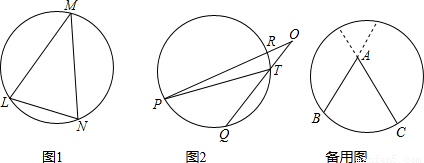
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com