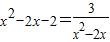【答案】
分析:當分式方程比較復雜時,通常采用換元法使分式方程簡化,可設u=x
2-2x.先求u,再求x,結果需檢驗,
解答:解:設x
2-2x=u,
原方程化為u-2=

,
兩邊同乘以u,并整理,得
u
2-2u-3=0,
(u-3)(u+1)=0,
∴u
1=3,u
2=-1.
當u
1=3時,x
2-2x-3=0,x
1=3,x
2=-1;
當u
2=-1時,x
2-2x+1=0,x
3,4=1.
經檢驗:x
l=3,x
2=-1,x
3,4=1都是原方程的根.
點評:當分式方程比較復雜時,通常采用換元法使分式方程簡化.