
【題目】已知:如圖①,在矩形ABCD中,AB=5,AD=![]() ,AE⊥BD,垂足是E.點F是點E關于AB的對稱點,連接AF、BF.
,AE⊥BD,垂足是E.點F是點E關于AB的對稱點,連接AF、BF.
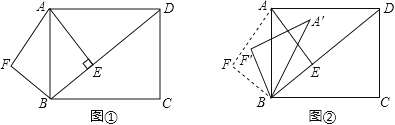
(1)求AE和BE的長;
(2)若將△ABF沿著射線BD方向平移,設平移的距離為m(平移距離指點B沿BD方向所經過的線段長度).當點F分別平移到線段AB、AD上時,直接寫出相應的m的值.
(3)如圖②,將△ABF繞點B順時針旋轉一個角α(0°<α<180°),記旋轉中的△ABF為△A′BF′,在旋轉過程中,設A′F′所在的直線與直線AD交于點P,與直線BD交于點Q.是否存在這樣的P、Q兩點,使△DPQ為等腰三角形?若存在,求出此時DQ的長;若不存在,請說明理由.
【答案】(1)4,3;(2)3或![]() .(3)DQ的長度分別為
.(3)DQ的長度分別為![]() 、
、![]() ;
;![]() 或
或![]() .
.
【解析】試題分析:(1)利用矩形性質、勾股定理及三角形面積公式求解;
(2)依題意畫出圖形,如答圖2所示.利用平移性質,確定圖形中的等腰三角形,分別求出m的值;
(3)在旋轉過程中,等腰△DPQ有4種情形,如答圖3所示,對于各種情形分別進行計算.
試題解析:(1)在Rt△ABD中,AB=5,AD=![]() ,
,
由勾股定理得:BD=![]() =
=![]() =
=![]() .
.
∵![]() =
=![]() BDAE=
BDAE=![]() ABAD,
ABAD,
∴AE=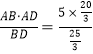 =4.
=4.
在Rt△ABE中,AB=5,AE=4,
由勾股定理得:BE=3;
(2)設平移中的三角形為△A′B′F′,如答圖2所示:
由對稱點性質可知,∠1=∠2.
由平移性質可知,AB∥A′B′,∠4=∠1,BF=B′F′=3.
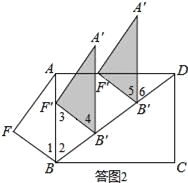
①當點F′落在AB上時,
∵AB∥A′B′,
∴∠3=∠4,
∴∠3=∠2,
∴BB′=B′F′=3,即m=3;
②當點F′落在AD上時,
∵AB∥A′B′,
∴∠6=∠2,
∵∠1=∠2,∠5=∠1,
∴∠5=∠6,
又易知A′B′⊥AD,
∴△B′F′D為等腰三角形,
∴B′D=B′F′=3,
∴BB′=BD﹣B′D=![]() ﹣3=
﹣3=![]() ,即m=
,即m=![]() ;
;
(3)存在.理由如下:
在旋轉過程中,等腰△DPQ依次有以下4種情形:
①如答圖3﹣1所示,點Q落在BD延長線上,且PD=DQ,易知∠2=2∠Q,
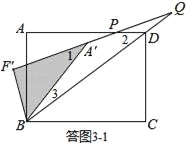
∵∠1=∠3+∠Q,∠1=∠2,
∴∠3=∠Q,
∴A′Q=A′B=5,
∴F′Q=F′A′+A′Q=4+5=9.
在Rt△BF′Q中,由勾股定理得:BQ=![]() =
=![]() .
.
∴DQ=BQ﹣BD=![]() ;
;
②如答圖3﹣2所示,點Q落在BD上,且PQ=DQ,易知∠2=∠P,
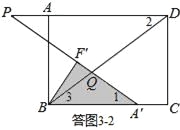
∵∠1=∠2,
∴∠1=∠P,
∴BA′∥PD,則此時點A′落在BC邊上.
∵∠3=∠2,
∴∠3=∠1,
∴BQ=A′Q,
∴F′Q=F′A′﹣A′Q=4﹣BQ.
在Rt△BQF′中,由勾股定理得:![]() ,
,
即![]() ,
,
解得:BQ=![]() ,
,
∴DQ=BD﹣BQ=![]() =
=![]() ;
;
③如答圖3﹣3所示,點Q落在BD上,且PD=DQ,易知∠3=∠4.
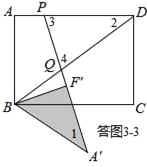
∵∠2+∠3+∠4=180°,∠3=∠4,
∴∠4=90°﹣![]() ∠2.
∠2.
∵∠1=∠2,
∴∠4=90°﹣![]() ∠1.
∠1.
∴∠A′QB=∠4=90°﹣![]() ∠1,
∠1,
∴∠A′BQ=180°﹣∠A′QB﹣∠1=90°﹣![]() ∠1,
∠1,
∴∠A′QB=∠A′BQ,
∴A′Q=A′B=5,
∴F′Q=A′Q﹣A′F′=5﹣4=1.
在Rt△BF′Q中,由勾股定理得:BQ=![]() =
=![]() ,
,
∴DQ=BD﹣BQ=![]() ;
;
④如答圖3﹣4所示,點Q落在BD上,且PQ=PD,易知∠2=∠3.
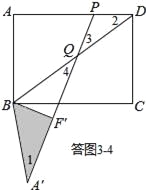
∵∠1=∠2,∠3=∠4,∠2=∠3,
∴∠1=∠4,
∴BQ=BA′=5,
∴DQ=BD﹣BQ=![]() ﹣5=
﹣5=![]() .
.
綜上所述,存在4組符合條件的點P、點Q,使△DPQ為等腰三角形;
DQ的長度分別為![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,把Rt△ABC放在直角坐標系內,其中∠CAB=90°,BC=5,點A,B的坐標分別為(1,0)、(4,0).將△ABC沿x軸向右平移,當點C落在直線y=2x﹣6上時,線段BC掃過的面積為( ) 
A.4
B.8
C.16
D.8 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車廠改進生產工藝后,每天生產的汽車比原來每天生產的汽車多6輛,那么現在15天的產量就超過了原來20天的產量.若設原來每天能生產x輛,則可列關于x的不等式為( )
A. 15x>20(x+6) B. 15(x+6)≥20x C. 15x>20( x-6) D. 15(x+6)>20x
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,E是直線AB,CD內部一點,AB∥CD,連接EA,ED.
(1)探究猜想: ①若∠A=20°,∠D=40°,求∠AED的度數
②猜想圖①中∠AED,∠EAB,∠EDC的關系,并用兩種不同的方法證明你的結論.
(2)拓展應用: 如圖②,射線FE與l1 , l2交于分別交于點E、F,AB∥CD,a,b,c,d分別是被射線FE隔開的4個區域(不含邊界,其中區域a,b位于直線AB上方,P是位于以上四個區域上的點,猜想:∠PEB,∠PFC,∠EPF的關系(任寫出兩種,可直接寫答案).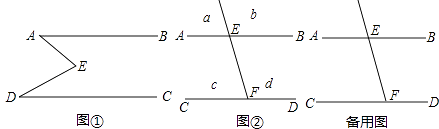
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面內的兩條直線有相交和平行兩種位置關系.
(1)如圖1,若AB∥CD,點P在AB,CD內部,∠B=50°,∠D=30°,求∠BPD. 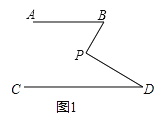
(2)如圖2,將點P移到AB,CD外部,則∠BPD,∠B,∠D之間有何數量關系?請證明你的結論. 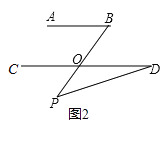
(3)如圖3,寫出∠BPD,∠B,∠D,∠BQD之間的數量關系?(不需證明) 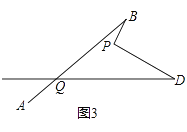
(4)如圖4,求出∠A+∠B+∠C+∠D+∠E+∠F的度數. 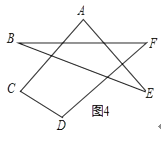
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養殖戶的養殖成本逐年增長,已知第一年的養殖成本為12萬元,第3年的養殖成本為17萬元.設每年平均增長的百分率為x,則下面所列方程中正確的是( )
A.12(1﹣x)2=17
B.17(1﹣x)2=12
C.17(1+x)2=12
D.12(1+x)2=17
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,將A、B、C三個字母隨機填寫在三個空格中(每空填一個字母,每空中的字母不重復),請你用畫樹狀圖或列表的方法求從左往右字母順序恰好是A、B、C的概率;
(2)若在如圖三個空格的右側增加一個空格,將A、B、C、D四個字母任意填寫其中(每空填一個字母,每空中的字母不重復),從左往右字母順序恰好是A、B、C、D的概率為 .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com