
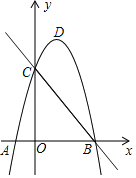
【題目】如圖,已知直線y1=﹣x+3與x軸交于點B,與y軸交于點C,拋物y2=ax2+bx+c經過點B,C并與x軸交于點A(﹣1,0).
(1)求拋物線解析式,并求出拋物線的頂點D坐標 ;
(2)當y2<0時、請直接寫出x的取值范圍 ;
(3)當y1<y2時、請直接寫出x的取值范圍 ;
(4)將拋物線y2向下平移,使得頂點D落到直線BC上,求平移后的拋物線解析式 .
【答案】(1)![]() ;(2)x<﹣1或x>3;(3)0<x<3;(4)y=x2+2x+1.
;(2)x<﹣1或x>3;(3)0<x<3;(4)y=x2+2x+1.
【解析】
(1)列方程得到C(0,3),B(3,0),設拋物線解析式為y=a(x+1)(x﹣3),列方程即可得到結論;
(2)由圖象即可得到結論;
(3)由圖象即可得到結論;
(4)當根據平移的性質即可得到結論.
解:(1)對于y1=﹣x+3,當x=0時,y=3,
∴C(0,3),
當y=0時,x=3,
∴B(3,0),
∵拋物線與x軸交于A(﹣1,0)、B(3,0)兩點,
設拋物線解析式為y=a(x+1)(x﹣3),
拋物線過點C(0,3),
∴3=a(0+1)(0﹣3),
解得:a=1,
∴y=(x+1)(x﹣3)=x+2x+3,
∴頂點D(1,4);
(2)由圖象知,當y2<0時、x的取值范圍為:x<﹣1或x>3;
(3)由圖象知當y1<y2時、x的取值范圍為:0<x<3;
(4)當x=1時,y=﹣1+3=2,
∵拋物線向下平移2個單位,
∴拋物線解析式為y=﹣x2+2x+3﹣2=﹣x2+2x+1.
故答案為:(1)(1,4);(2)x<﹣1或x>3;(3)0<x<3;(4)y=x2+2x+1.


科目:初中數學 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,將
的中點,將![]() 繞點
繞點![]() 逆時針旋轉至點
逆時針旋轉至點![]() 與點
與點![]() 重合,此時點
重合,此時點![]() 旋轉至
旋轉至![]() 處,則點
處,則點![]() 在旋轉過程中形成的
在旋轉過程中形成的![]() 、線段
、線段![]() 、點
、點![]() 在旋轉過程中形成的
在旋轉過程中形成的![]() 與線段
與線段![]() 所圍成的陰影部分的面積為( )
所圍成的陰影部分的面積為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象交于A(2,1),B(-1,
的圖象交于A(2,1),B(-1,![]() )兩點.
)兩點.

(1)求m、k、b的值;
(2)連接OA、OB,計算三角形OAB的面積;
(3)結合圖象直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
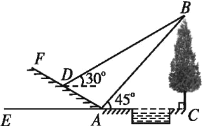
【題目】如圖所示,某數學活動小組選定測量小河對岸大樹BC的高度,他們在斜坡上D處測得大樹頂端B的仰角是30°,朝大樹方向下坡走6米到達坡底A處,在A處測得大樹頂端B的仰角是45°,若坡角∠FAE=30°,求大樹的高度(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,拋物線y=﹣4x2﹣8mx﹣m2+2m的頂點p.
(1)點p的坐標為 (含m的式子表示)
(2)當﹣1≤x≤1時,y的最大值為5,則m的值為多少;
(3)若拋物線與x軸(不包括x軸上的點)所圍成的封閉區域只含有1個整數點,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:有且僅有一組對角相等的凸四邊形叫做“準平行四邊形”.例如:凸四邊形![]() 中,若
中,若![]() ,則稱四邊形
,則稱四邊形![]() 為準平行四邊形.
為準平行四邊形.
(1)如圖①,![]() 是
是![]() 上的四個點,
上的四個點,![]() ,延長
,延長![]() 到
到![]() ,使
,使![]() .求證:四邊形
.求證:四邊形![]() 是準平行四邊形;
是準平行四邊形;
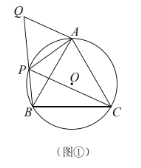
(2)如圖②,準平行四邊形![]() 內接于
內接于![]() ,
,![]() ,若
,若![]() 的半徑為
的半徑為![]() ,求
,求![]() 的長;
的長;

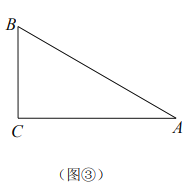
(3)如圖③,在![]() 中,
中,![]() ,若四邊形
,若四邊形![]() 是準平行四邊形,且
是準平行四邊形,且![]() ,請直接寫出
,請直接寫出![]() 長的最大值.
長的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:二次函數y=ax2+bx+![]() (a>0,b<0)的圖象與x軸只有一個公共點A.
(a>0,b<0)的圖象與x軸只有一個公共點A.
(1)當a=![]() 時,求點A的坐標;
時,求點A的坐標;
(2)求A點的坐標(只含b的代數式來表示);
(3)過點A的直線y=x+k與二次函數的圖象相交于另一點B,當b≥﹣1時,求點B的橫坐標m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
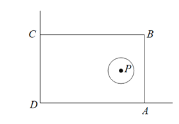
【題目】在美化校園的活動中,某興趣小組想借助如圖所示的直角墻角(兩邊足夠長),用26m長的籬笆圍成一個矩形花園ABCD(籬笆只圍AB,BC兩邊),設BC=x m.
(1)若矩形花園ABCD的面積為165m2,求 x的值;
(2)若在P處有一棵樹,樹中心P與墻CD,AD的距離分別是13m和6m,要將這棵樹圍在花園內(考慮到樹以后的生長,籬笆圍矩形ABCD時,需將以P為圓心,1為半徑的圓形區域圍在內),求矩形花園ABCD面積S的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com