
【題目】數軸上點A對應的數為![]() ,點B對應的數為
,點B對應的數為![]() ,且多項式
,且多項式![]() 的二次項系數為
的二次項系數為![]() ,常數項為
,常數項為![]() .
.
(1)直接寫出:![]() ;
;
(2)數軸上點A、B之間有一動點P,若點P對應的數為![]() ,試化簡
,試化簡![]() ;
;
(3)若點M從點A出發,以每秒1個單位長度的速度沿數軸向右移動;同時點N從點B出發,沿數軸每秒2個單位長度的速度向左移動,到達A點后立即返回并向右繼續移動,求經過多少秒后,M、N兩點相距1個單位長度?
【答案】(1)2,5;(2)x+8;(3)經過2秒或![]() 秒或7秒或8秒后,M、N兩點相距1個單位長度.
秒或7秒或8秒后,M、N兩點相距1個單位長度.
【解析】
(1)根據多項式的系數即可得出結論;
(2)先確定出x的范圍,進而得出2x+4>0,x5<0,6x>0,最后去掉絕對值,合并即可得出結論;
(3)分點N未到達點A之前和之后,建立方程求解即可得出結論.
(1)∵多項式6x3y2xy+5的二次項系數為a,常數項為b,
∴a=2,b=5,
故答案為:2,5;
(2)∴數軸上點A對應的數為a,點B對應的數為b,
∴數軸上點A對應的數為2,點B對應的數為5,
∵數軸上點A、B之間有一動點P,點P對應的數為x,
∴2<x<5,
∴2x+4>0,x5<0,6x>0,
∴|2x+4|+2|x5||6x|=2x+42(x5)(6x)=2x+42x+106+x=x+8;
(3)設經過t秒后,M、N兩點相距1個單位長度,
由運動知,AM=t,BN=2t,
①當點N到達點A之前時,
a、當M,N相遇前,M、N兩點相距1個單位長度,
∴t+1+2t=5+2,
∴t=2秒,
b、當M,N相遇后,M、N兩點相距1個單位長度,
∴t+2t1=5+2,
∴t=![]() 秒,
秒,
②當點N到達點A之后時,
a、當N未追上M時,M、N兩點相距1個單位長度,
∴t[2t(5+2)]=1,
∴t=7秒;
b、當N追上M后時,M、N兩點相距1個單位長度,
∴[2t(5+2)]t=1,
∴t=8秒;
即:經過2秒或![]() 秒或7秒或8秒后,M、N兩點相距1個單位長度.
秒或7秒或8秒后,M、N兩點相距1個單位長度.


科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C是⊙O上一點,連接AC,∠MAC=∠CAB,作CD⊥AM,垂足為D. 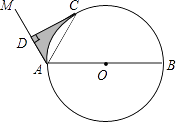
(1)求證:CD是⊙O的切線;
(2)若∠ACD=30°,AD=4,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線 ![]() (
( ![]() <
< ![]() <0)與x軸最多有一個交點,現有以下結論:
<0)與x軸最多有一個交點,現有以下結論:
① ![]() <0;②該拋物線的對稱軸在y軸左側;③關于x的方程
<0;②該拋物線的對稱軸在y軸左側;③關于x的方程 ![]() 有實數根;④對于自變量x的任意一個取值,都有
有實數根;④對于自變量x的任意一個取值,都有 ![]() ,其中正確的為( )
,其中正確的為( )
A.①②
B.①②④
C.①②③
D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在已知線段AB的同側構造∠FAB=∠GBA,并且在射線AF,BG上分別取點D和E,在線段AB上取點C,連結DC和EC.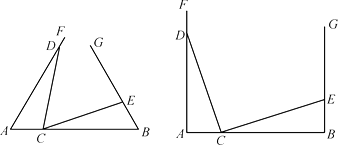
Ⅰ、如圖,若AD=3,BE=1,△ADC≌△BCE.在∠FAB=∠GBA=60或∠FAB=∠GBA=90兩種情況中任選一種,解決以下問題:
①線段AB的長度是否發生變化,直接寫出長度或變化范圍;
②∠DCE的度數是否發生變化,直接寫出度數或變化范圍.
Ⅱ、若AD=a,BE=b,∠FAB=∠GBA=α,且△ADC和△BCE這兩個三角形全等,請求出:
①線段AB的長度或取值范圍,并說明理由;
②∠DCE的度數或取值范圍,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在梯形紙片ABCD中,AD//BC,AD>CD,將紙片沿過點D的直線折疊,使點C落在AD上的點C處,折痕DE交BC于點E,連結C′E.
求證:四邊形CDC′E是菱形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某運動品牌對第一季度A、B兩款運動鞋的銷售情況進行統計,兩款運動鞋的銷售量及總銷售額如圖10所示:
(1)一月份B款運動鞋的銷售量是A款的![]() ,則一月份B款運動鞋銷售了多少雙?
,則一月份B款運動鞋銷售了多少雙?
(2)第一季度這兩款運動鞋的銷售單價保持不變,求三月份的總銷售額(銷售額=銷售單價×銷售量);
(3)結合第一季度的銷售情況,請你對這兩款運動鞋的進貨、銷售等方面提出一條建議。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的口袋里裝有若干個相同的紅球,為了估計袋中紅球的數量,某學習小組做了摸球實驗,他們將30個與紅球大小形狀完全相同的白球裝入袋中,攪勻后從中隨機摸出一個球并記下顏色,再把它放回袋中,不斷重復.下表是幾次活動匯總后統計的數據:

(1)請估計:當次數s很大時,摸到白球的頻率將會接近 ;假如你去摸一次,你摸到白球的概率是 (精確到0.1).
(2)試估算口袋中紅球有多少只?
(3)解決了上面的問題后請你從統計與概率方面談一條啟示.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是正方形ABCD的邊DC上一點,把△ADE順時針旋轉△ABF的位置. 
(1)旋轉中心是點 , 旋轉角度是度;
(2)若連結EF,則△AEF是三角形;并證明;
(3)若四邊形AECF的面積為25,DE=2,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線l:y=﹣ ![]() x+6交y軸于點A,與x軸交于點B,過A、B兩點的拋物線m與x軸的另一個交點為C,(C在B的左邊),如果BC=5,求拋物線m的解析式,并根據函數圖像指出當m的函數值大于0的函數值時x的取值范圍.
x+6交y軸于點A,與x軸交于點B,過A、B兩點的拋物線m與x軸的另一個交點為C,(C在B的左邊),如果BC=5,求拋物線m的解析式,并根據函數圖像指出當m的函數值大于0的函數值時x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com