
【題目】在一次海上救援中,兩艘專業救助船![]() 同時收到某事故漁船的求救訊息,已知此時救助船
同時收到某事故漁船的求救訊息,已知此時救助船![]() 在
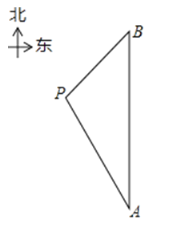
在![]() 的正北方向,事故漁船
的正北方向,事故漁船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故漁船
的西南方向上,且事故漁船![]() 與救助船
與救助船![]() 相距120海里.
相距120海里.
(1)求收到求救訊息時事故漁船![]() 與救助船
與救助船![]() 之間的距離;
之間的距離;
(2)若救助船A,![]() 分別以40海里/小時、30海里/小時的速度同時出發,勻速直線前往事故漁船
分別以40海里/小時、30海里/小時的速度同時出發,勻速直線前往事故漁船![]() 處搜救,試通過計算判斷哪艘船先到達.
處搜救,試通過計算判斷哪艘船先到達.
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
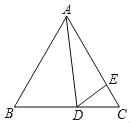
【題目】如圖,等邊△ABC中,D為BC邊上一點,E為AC邊上一點,∠ADE=60°
(1)求證:△ABD∽△DCE;
(2)若BD=4,CE=![]() ,求△ABC的邊長.
,求△ABC的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司研制出新產品,該產品的成本為每件2400元.在試銷期間,購買不超過10件時,每件銷售價為3000元;購買超過10件時,每多購買一件,所購產品的銷售單價均降低5元,但最低銷售單價為2600元。請解決下列問題:
(1)直接寫出:購買這種產品 ________件時,銷售單價恰好為2600元;
(2)設購買這種產品x件(其中x>10,且x為整數),該公司所獲利潤為y元,求y與x之間的函數表達式;
(3)該公司的銷售人員發現:當購買產品的件數超過10件時,會出現隨著數量的增多,公司所獲利潤反而減少這一情況.為使購買數量越多,公司所獲利潤越大,公司應將最低銷售單價調整為多少元?(其它銷售條件不變)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2﹣2(k﹣1)x+2.
(1)當k=3時,求函數圖象與x軸的交點坐標;
(2)函數圖象的對稱軸與原點的距離為2,當﹣1≤x≤5時,求此時函數的最小值;
(3)函數圖象交y軸于點B,交直線x=4于點C,設二次函數圖象上的一點P(x,y)滿足0≤x≤4時,y≤2,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“五一”期間,小華和媽媽到某景區游玩,小明想利用所學的數學知識,估測景區里的觀景塔![]() 的高度,他從點
的高度,他從點![]() 處的觀景塔出來走到點
處的觀景塔出來走到點![]() 處.沿著斜坡
處.沿著斜坡![]() 從
從![]() 點走了
點走了![]() 米到達
米到達![]() 點,此時回望觀景塔,更顯氣勢宏偉.在
點,此時回望觀景塔,更顯氣勢宏偉.在![]() 點觀察到觀景塔頂端的仰角為
點觀察到觀景塔頂端的仰角為![]() 且
且![]() ,再往前走到
,再往前走到![]() 處,觀察到觀景塔頂端的仰角
處,觀察到觀景塔頂端的仰角![]() ,測得
,測得![]() 之間的水平距離
之間的水平距離![]() 米,則觀景塔的高度
米,則觀景塔的高度![]() 約為( ) 米. (
約為( ) 米. (![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
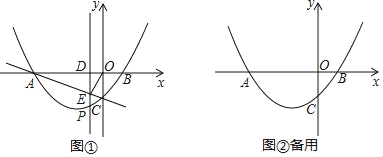
【題目】如圖,拋物線y=![]() 與x軸分別交于A、B兩點(點A在點B的左側,)與y軸交于點C,作直線AC.
與x軸分別交于A、B兩點(點A在點B的左側,)與y軸交于點C,作直線AC.
(1)點B的坐標為 ,直線AC的關系式為 .
(2)設在直線AC下方的拋物線上有一動點P,過點P作PD⊥x軸于D,交直線AC于點E,當CE平分∠OEP時求點P的坐標.
(3)點M在x軸上,點N在拋物線上,試問以點A、C、M、N為頂點的四邊形能否成為平行四邊形?若存在,直接寫出所有點M的坐標;若不存在,請簡述你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=14x2+1(如圖所示).
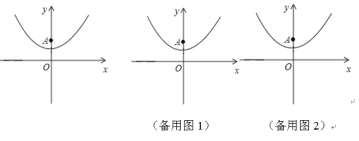
(1)填空:拋物線的頂點坐標是(___,___),對稱軸是___;
(2)已知y軸上一點A(0,2),點P在拋物線上,過點P作PB⊥x軸,垂足為B. 若△PAB是等邊三角形,求點P的坐標;
(3)在(2)的條件下,點M在直線AP上。在平面內是否存在點N,使四邊形OAMN為菱形?若存在,直接寫出所有滿足條件的點N的坐標;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在Rt△ABC中,斜邊AC的中點M關于BC的對稱點為點O,將△ABC繞點O順時針旋轉至△DCE,連接BD,BE,
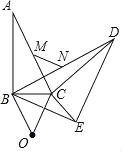
(1)在①∠BOE,②∠ACD,③∠COE中,等于旋轉角的是 (填寫序號即可);
(2)判斷∠A和∠BEC的數量關系,并證明;
(3)點N是BD的中點,連接MN,若MN=2,求BE的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com