
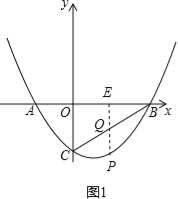
【題目】如圖,拋物線y=ax2+bx﹣2與x軸交于A、B兩點,與y軸交于點C,已知A(﹣1,0),且tan∠ABC=![]() .
.
(1)求拋物線的解折式.
(2)在直線BC下方拋物線上一點P,當四邊形OCPB的面積取得最大值時,求此時點P的坐標.
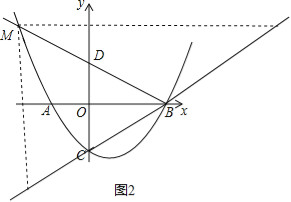
(3)在y軸的左側拋物線上有一點M,滿足∠MBA=∠ABC,若點N是直線BC上一點,當△MNB為等腰三角形時,求點N的坐標.

【答案】(1)拋物線的解折式為y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)P點的坐標為(![]() ,﹣
,﹣![]() );
);
(3)點N的坐標為(﹣2,﹣ ![]() )或(8,
)或(8, ![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).
【解析】試題分析:(1)由解析式求得C的坐標,然后根據tan∠ABC=![]() 求得OB=3,從而求得B的坐標,進而根據待定系數法即可求得解析式;
求得OB=3,從而求得B的坐標,進而根據待定系數法即可求得解析式;
(2)過點P作y軸的平行線與BC交于點Q,與OB交于點E,設P(x,x2﹣2x﹣3),易得,直線BC的解析式為y=x﹣3則Q點的坐標為(x,x﹣3),再根據S四邊形ABPC=S△ABC+S△BPQ+S△CPQ即可得出結論.
(3)根據題意求得M的坐標,然后分三種情況討論求得即可.
解:(1)由拋物線y=ax2+bx﹣2可知C的坐標為(0,﹣2),
∴OC=2,
∵tan∠ABC=![]() =
=![]()
∴OB=3,
∴B(3,0),
∵A(﹣1,0),
把A、B的坐標代入y=ax2+bx﹣2得:
![]()
解得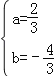 ,
,
∴拋物線的解折式為y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)過點P作y軸的平行線與BC交于點Q,與OB交于點E,
設P(x,![]() x2﹣
x2﹣![]() x﹣2),
x﹣2),
設直線BC的解析式為y=kx+b(k≠0),
∵B(3,0),C(0,﹣2),
∴![]() ,
,
解得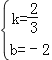 ,
,
∴直線BC的解析式為y=![]() x﹣2.
x﹣2.
∴Q點的坐標為(x,![]() x﹣2),
x﹣2),
∴S四邊形ABPC=S△ABC+S△BPQ+S△CPQ
=![]() ABOC+
ABOC+![]() QPOE+
QPOE+![]() QPEB
QPEB
=![]() ×4×2+
×4×2+![]() (2x﹣
(2x﹣![]() x2)×3
x2)×3
=﹣x2+3x+4
=﹣(x﹣![]() )2+
)2+![]() ,
,
∴當x=![]() 時,四邊形ABPC的面積最大,最大面積為
時,四邊形ABPC的面積最大,最大面積為![]() .此時P點的坐標為(
.此時P點的坐標為(![]() ,﹣
,﹣![]() ).
).
(3)設直線AM交y軸于D,
∵∠MBA=∠ABC,
∴OD=OC=2,
∴D(0,2),
設直線AM的解析式為y=mx+2,
代入B(3,0)得0=3m+2,解得m=﹣![]() ,
,
∴直線AM的解析式為y=﹣![]() x+2,
x+2,
解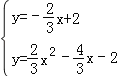 得
得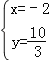 或
或![]() ,
,
∴M(![]() ),
),
設N(x,![]() x﹣2),
x﹣2),
∵BM2=(3+2)2+(![]() )2,MN2=(x+2)2+(
)2,MN2=(x+2)2+(![]() x﹣2﹣
x﹣2﹣![]() )2,BN2=(x﹣3)2+(
)2,BN2=(x﹣3)2+(![]() x﹣2)2,
x﹣2)2,
當MB=BN時,N(﹣2,﹣![]() )或(8,
)或(8,![]() );
);
當MB=MN時,則(3+2)2+(![]() )2=(x+2)2+(
)2=(x+2)2+(![]() x﹣2﹣
x﹣2﹣![]() )2,
)2,
整理得13x2﹣28x﹣33=0,
解得x1=3,x2=﹣![]() ,
,
∴N(﹣![]() ,﹣
,﹣![]() );
);
當BN=MN時,(x+2)2+(![]() x﹣2﹣
x﹣2﹣![]() )2=(x﹣3)2+(
)2=(x﹣3)2+(![]() x﹣2)2,
x﹣2)2,
整理得10x=﹣35,
解得x=﹣![]()
∴N(﹣![]() ,﹣
,﹣![]() );
);
綜上,點N的坐標為(﹣2,﹣![]() )或(8,
)或(8,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).


科目:初中數學 來源: 題型:
【題目】已知三角形的兩邊長是2 cm,3 cm,則該三角形的周長l的取值范圍是( )
A. 1<l<5 B. 1<l<6
C. 5<l<9 D. 6<l<10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】花粉的質量很小,一粒某種植物花粉的質量約為0.000037 mg,已知1 g=1 000 mg,那么0.000 037 mg用科學記數法表示為( )
A. 3.7×10-5 g B. 3.7×10-6 g C. 3.7×10-7 g D. 3.7×10-8 g
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com