
【題目】(1)已知 y y1 y2 ,而 y1與 x 1成正比例, y2與 x2 成正比例,并且x 1 時,y 2;x 0 時,y 2,求y與x的函數關系式;
(2)如圖,直線 y 2 x 3 與 x 軸相交于點 A,與 y 軸相交于點 B.
①求 A、B 兩點的坐標;
②過 B 點作直線 BP 與 x 軸相交于 P,且使 AP=2OA,求△BOP 的面積。

【答案】(1)y=-2x2+2x+2;
(2)①A(![]() ,0) B(0,3);
,0) B(0,3);
②![]() 或
或![]()
【解析】
(1)根據正比例的定義設出y與x之間的函數關系式,然后利用待定系數法求函數解析式即可得解;
(2)令y=0即可求出點A的橫坐標,令x=0即可求出點B的縱坐標;
(3)分點P在點A的左側和右側兩種情況求解即可.
解:(1)∵y1與x+1成正比例,y2與x2成正比例
設y1=a(x+1),y2=bx2,
∴y=a(x+1)+bx2,
∵x 1 時,y 2;x 0 時,y 2,
∴![]() ,
,
解得![]() ,
,
∴y=2(x+1)-2x2=-2x2+2x+2;
(2)①∵y=2x+3,
∴當y=0時,x=![]() ;當x=0時,y=3,
;當x=0時,y=3,
∴A(![]() ,0) B(0,3);
,0) B(0,3);
②當P在A左側時,AP=2OA=3,OP=OA+AP=![]() ,
,
∴S△BOP=![]() ×3×
×3×![]() =
=![]() ;
;
當P在A右側時,AP=2OA=3,OP=AP-OA=![]() ,
,
∴S△BOP=![]() ×3×
×3×![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】為慶祝祖國70華誕,某小區計劃在一塊面積為196m2的正方形空地上建一個面積為100m2的長方形花壇(長方形的邊與正方形空地的邊平行),要求長方形的長是寬的2倍.請你通過計算說明該小區能否實現這個愿望?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,D為AB的中點,F為BC上一點,DF∥AC,延長FD至E,且DE=DF,聯結AE、AF

(1)求證:∠E=∠C;
(2)如果DF平分∠AFB,求證:AC⊥AB
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是方城縣潘河的某一段,現要測量河的寬度(即河兩岸相對的兩點A、B間的距離),先在AB的垂線BF上取兩點C、D,使BC=CD,再定出BF的垂線DE,使點A、C、E在同一條直線上,直接在河岸上測量DE的長度就知道河的寬度AB了,你知道這是為什么嗎?請先判斷DE和AB大小關系,然后說明理由.
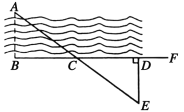
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】楊陽同學沿一段筆直的人行道行走,在由A步行到達B處的過程中,通過隔離帶的空隙O,剛好瀏覽完對面人行道宣傳墻上的社會主義核心價值觀標語,其具體信息匯集如下:
如圖,AB∥OH∥CD,相鄰兩平行線間的距離相等,AC,BD相交于O,OD⊥CD.垂足為D,已知AB=20米,請根據上述信息求標語CD的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)a2(﹣a4)+2(a2)3
(2)(2x﹣1)(2x+1)﹣(x﹣6)(4x+3)
(3)(2x﹣3y)2+2(y+3x)(3x﹣y)
(4)(a﹣2b+3)(a+2b+3)
(5) ![]()
(6)(2m+3n)(2m﹣n)﹣2n(2m﹣n)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一倉庫為了保持庫內的濕度和溫度,四周墻上均裝有如圖所示的自動通風設施,該設施的下部ABCD是矩形,其中AB=2米,BC=![]() 米,上部△CDG是等邊三角形,固定點E為AB的中點。△EMN是由電腦控制其變化的三角通風窗(陰影部分均不通風),MN(MN可與CD重合)是可以沿設施邊框上下滑動且始終保持與AB平行的伸縮橫桿。(當MN在DC上方時,MD的長度是MN到DC距離的
米,上部△CDG是等邊三角形,固定點E為AB的中點。△EMN是由電腦控制其變化的三角通風窗(陰影部分均不通風),MN(MN可與CD重合)是可以沿設施邊框上下滑動且始終保持與AB平行的伸縮橫桿。(當MN在DC上方時,MD的長度是MN到DC距離的![]() 倍)
倍)

(1)當MN和AB之間的距離為0.5米時,求此時 △EMN的面積;
(2)設MN與AB之間的距離為x米,求△EMN的面積S(平方米)與x的函數關系式;
(3)探究△EMN的面積S(平方米)有無最大值,若有,求出這個最大值;若無,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com