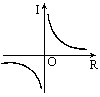
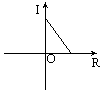
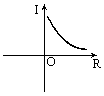
如圖，在公式I＝
中，當電壓U一定時，電流I與電阻R之間的函數關系可用圖像表示為
[ ]
科目：初中數學 來源：吉林省長春外國語學校2011-2012學年八年級第一次月考數學試題 題型：044
我們已經知道了一些特殊的勾股數，如三個連續整數中的勾股數：3、4、5；三個連續的偶數中的勾股數6、8、10；由此發現勾股數的正整數倍仍然是勾股數．
(1)如果a、b、c是一組勾股數，即滿足a2＋b2＝c2，求證：ka、kb、kc(k為正整數)也是一組勾股數．
(2)另外利用一些構成勾股數的公式也可以寫出許多勾股數，如
①公式a＝m2－n2，b＝2mn，c＝m2＋n2(m、n為整數，m＞n，m＞1)
②世界上第一次給出的勾股數的公式，被收集在《九章算術》中a＝
(m2－n2)，b＝mn，c＝
(m2＋n2)(m、n為正整數，m＞n)
③公元前427－公元前347，由柏拉圖提出的公式a＝n2－1，b＝2n，c＝n2＋1(n＞1，且n為整數)
④畢達哥拉斯學派提出的公式a＝2n＋1，b＝2n2＋2n，c＝2n2＋2n＋1(n為正整數)
請你在上述的四個公式中選擇一種加以證明，滿足公式的a、b、c是一組勾股數
(3)請根據你在(2)中所選的公式寫出一組勾股數．
查看答案和解析>>
科目：初中數學 來源：2013年吉林省長春市高級中等學校招生考試數學 題型：044
如圖，在平面直角坐標系中，拋物線y＝ax2＋bx－2與x軸交于點A(－1，0)、B(4，0)．點M、N在x軸上，點N在點M右側，MN＝2．以MN為直角邊向上作等腰直角三角形CMN，∠CMN＝90°．設點M的橫坐標為m．
(1)求這條拋物線所對應的函數關系式．
(2)求點C在這條拋物線上時m的值．
(3)將線段CN繞點N逆時針旋轉90°后，得到對應線段DN．
①當點D在這條拋物線的對稱軸上時，求點D的坐標．
②以DN為直角邊作等腰直角三角形DNE，當點E在這條拋物線的對稱軸上時，直接寫出所有符合條件的m值．
［參考公式：拋物線y＝ax2＋bx＋c(a≠0)的頂點坐標為
］
查看答案和解析>>
科目：初中數學 來源：2013屆江蘇省南京市鼓樓區中考二模數學試卷（帶解析） 題型：解答題
【提出問題】
如圖①，在梯形ABCD中，AD//BC，AC、BD交于點E，∠BEC＝n°，若AD＝a，BC＝b，則梯形ABCD的面積最大是多少？
【探究過程】
小明提出：可以從特殊情況開始探究，如圖②，在梯形ABCD中，AD//BC，AC⊥BD，若AD＝3，BC＝7，則梯形ABCD的面積最大是多少？
如圖③，過點D做DE//AC交BC的延長線于點E，那么梯形ABCD的面積就等于△DBE的面積，求梯形ABCD的面積最大值就是求△DBE的面積最大值．如果設AC＝x，BD＝y，那么S△DBE＝xy．
以下是幾位同學的對話：
A同學：因為y＝
，所以S△DBE＝x，求這個函數的最大值即可．
B同學：我們知道x2＋y2＝100，借助完全平方公式可求S△DBE＝xy的最大值
C同學：△DBE是直角三角形，底BE＝10，只要高最大，S△DBE就最大，我們先將所有滿足BE＝10的直角△DBE都找出來，然后在其中尋找高最大的△DBE即可．
（1）請選擇A同學或者B同學的方法，完成解題過程．
（2）請幫C同學在圖③中畫出所有滿足條件的點D，并標出使△DBE面積最大的點D1．（保留作圖痕跡，可適當說明畫圖過程）
【解決問題】
根據對特殊情況的探究經驗，請在圖①中畫出面積最大的梯形ABCD的頂點D1，并直接寫出梯形ABCD面積的最大值．
查看答案和解析>>
科目：初中數學 來源：2012-2013學年江蘇省南京市鼓樓區中考二模數學試卷（解析版） 題型：解答題
【提出問題】
如圖①，在梯形ABCD中，AD//BC，AC、BD交于點E，∠BEC＝n°，若AD＝a，BC＝b，則梯形ABCD的面積最大是多少？
【探究過程】
小明提出：可以從特殊情況開始探究，如圖②，在梯形ABCD中，AD//BC，AC⊥BD，若AD＝3，BC＝7，則梯形ABCD的面積最大是多少？
如圖③，過點D做DE//AC交BC的延長線于點E，那么梯形ABCD的面積就等于△DBE的面積，求梯形ABCD的面積最大值就是求△DBE的面積最大值．如果設AC＝x，BD＝y，那么S△DBE＝xy．
以下是幾位同學的對話：
A同學：因為y＝
，所以S△DBE＝x，求這個函數的最大值即可．
B同學：我們知道x2＋y2＝100，借助完全平方公式可求S△DBE＝xy的最大值
C同學：△DBE是直角三角形，底BE＝10，只要高最大，S△DBE就最大，我們先將所有滿足BE＝10的直角△DBE都找出來，然后在其中尋找高最大的△DBE即可．
（1）請選擇A同學或者B同學的方法，完成解題過程．
（2）請幫C同學在圖③中畫出所有滿足條件的點D，并標出使△DBE面積最大的點D1．（保留作圖痕跡，可適當說明畫圖過程）
【解決問題】
根據對特殊情況的探究經驗，請在圖①中畫出面積最大的梯形ABCD的頂點D1，并直接寫出梯形ABCD面積的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
