
【題目】隨著綠城南寧近幾年城市建設的快速發展,對花木的需求量逐年提高.某園林專業戶計劃投資種植花卉及樹木,根據市場調查與預測,種植樹木的利潤![]() 與投資量
與投資量![]() 成正比例關系,如圖(1)所示;種植花卉的利潤
成正比例關系,如圖(1)所示;種植花卉的利潤![]() 與投資量
與投資量![]() 成二次函數關系,如圖(2)所示(注:利潤與投資量的單位:萬元)
成二次函數關系,如圖(2)所示(注:利潤與投資量的單位:萬元)

(1)分別求出利潤![]() 與
與![]() 關于投資量
關于投資量![]() 的函數關系式;
的函數關系式;
(2)如果這位專業戶以8萬元資金投入種植花卉和樹木,他至少獲得多少利潤?他能獲取的最大利潤是多少?
【答案】(1)y1=2x(x≥0);y=![]() x2(x≥0);(2)當x=8時,z的最大值是32.
x2(x≥0);(2)當x=8時,z的最大值是32.
【解析】
試題分析:(1)可根據圖象利用待定系數法求解函數解析式;
(2)根據總利潤=樹木利潤+花卉利潤,列出函數關系式,再求函數的最值.
試題解析:(1)設y1=kx,由圖①所示,函數y1=kx的圖象過(1,2),
所以2=k1,k=2,
故利潤y1關于投資量x的函數關系式是y1=2x(x≥0);
∵該拋物線的頂點是原點,
∴設y2=ax2,
由圖②所示,函數y2=ax2的圖象過(2,2),
∴2=a22,a=![]() ,
,
故利潤y2關于投資量x的函數關系式是:y=![]() x2(x≥0);
x2(x≥0);
(2)設這位專業戶投入種植花卉x萬元(0≤x≤8),則投入種植樹木(8-x)萬元,他獲得的利潤是z
元,根據題意,
得z=2(8-x)+![]() x2=
x2=![]() x2-2x+16=
x2-2x+16=![]() (x-2)2+14,
(x-2)2+14,
當x=2時,z的最小值是14,
∵0≤x≤8,
∴-2≤x-2≤6,
∴(x-2)2≤36,
∴![]() (x-2)2≤18,
(x-2)2≤18,
∴![]() (x-2)2+14≤18+14=32,
(x-2)2+14≤18+14=32,
即z≤32,此時x=8,
答:當x=8時,z的最大值是32.


科目:初中數學 來源: 題型:
【題目】如圖,長方體紙箱的長、寬、高分別為50cm、30cm、60cm,一只螞蟻從點A處沿著紙箱的表面爬到點B處.螞蟻爬行的最短路程為_______cm.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究;
(![]() )如圖,
)如圖, ![]() 、
、![]() 為
為![]() 的邊
的邊![]() 、
、![]() 上的兩定點,在
上的兩定點,在![]() 上求作一點
上求作一點![]() ,使
,使![]() 的周長最短.(不寫作法)
的周長最短.(不寫作法)

(![]() )如圖,矩形
)如圖,矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分別為邊
分別為邊![]() 、
、![]() 的中點,點
的中點,點![]() 、
、![]() 分別為
分別為![]() 、
、![]() 上的動點,求四邊形
上的動點,求四邊形![]() 周長的最小值.
周長的最小值.

(![]() )如圖,正方形
)如圖,正方形![]() 的邊長為
的邊長為![]() ,點
,點![]() 為
為![]() 邊中點,在邊
邊中點,在邊![]() 、
、![]() 、
、![]() 上分別確定點
上分別確定點![]() 、
、![]() 、
、![]() .使得四邊形
.使得四邊形![]() 周長最小,并求出最小值.
周長最小,并求出最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形紙片ABCD中,已知AD=8,AB=6,E是邊BC上的點,以AE為折痕折疊紙片,使點B落在點F處,連接FC,當△EFC為直角三角形時,BE的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A(3,﹣5)向上平移4個單位,再向左平移3個單位到點B,則點B的坐標為( )
A.(1,﹣8)B.(1,﹣2)C.(﹣7,﹣1)D.(0,﹣1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數的圖象經過點![]() ,且與正比例函數
,且與正比例函數![]() 的圖象相交于點
的圖象相交于點![]() ,與x軸相交于點
,與x軸相交于點![]()
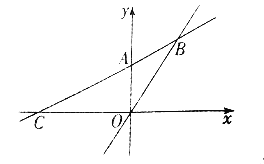
(1)求m的值及一次函數的表達式.
(2)求△BOC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在邊長為a的正方形的一角減去一個邊長為的小正方形(a>b),如圖①

① ②
(1)由圖①得陰影部分的面積為 .
(2)沿圖①中的虛線剪開拼成圖②,則圖②中陰影部分的面積為 .
(3)由(1)(2)的結果得出結論: = .
(4)利用(3)中得出的結論計算:20172-20162
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com