
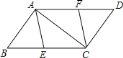
【題目】如圖,點![]() 、
、![]() 分別是
分別是![]() 的邊
的邊![]() 、
、![]() 上的點,
上的點,![]() 平分
平分![]() 、
、![]() 平分
平分![]() .
.

![]() 求證:
求證:![]() ;
;
![]() 若
若![]() ,
,![]() ,求證:四邊形
,求證:四邊形![]() 是菱形.
是菱形.
【答案】(1)證明見解析;(2)證明見解析.
【解析】
(1)由平行四邊形的性質可得AB=CD,AD=BC,且∠B=∠D,再由CE=AF,可得BE=DF,即可利用SAS定理判定△ABE≌△CDF;
(2)首先證明四邊形AECF是平行四邊形,再根據AE=BE,可得∠ABE=∠BAE,由∠BAC=90°可得∠ABE+∠ACE=90°,∠BAE+∠EAC=90°,再根據等角的余角相等可得∠ACE=∠EAC,進而得到AE=EC,由一組鄰邊相等的平行四邊形是菱形證出結論.
證明:![]() ∵四邊形
∵四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() 、
、![]() 平分
平分![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中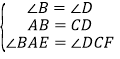 ,
,
∴![]() ;
;
![]() ∵四邊形
∵四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,
∵![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,
∴![]() ,
,
∴平行四邊形![]() 是菱形.
是菱形.
∴四邊形![]() 是菱形.
是菱形.


 階梯計算系列答案
階梯計算系列答案科目:初中數學 來源: 題型:
【題目】若所求的二次函數圖象與拋物線![]() 有相同的頂點,并且在對稱軸的左側,
有相同的頂點,并且在對稱軸的左側,![]() 隨
隨![]() 的增大而增大,在對稱軸的右側,
的增大而增大,在對稱軸的右側,![]() 隨
隨![]() 的增大而減小,則所求二次函數的解析式為( )
的增大而減小,則所求二次函數的解析式為( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分線BE交AC的延長線于點E.
(1)求∠CBE的度數;
(2)過點D作DF∥BE,交AC的延長線于點F,求∠F的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 從
從![]() 開始沿折線
開始沿折線![]() 以
以![]() 的速度運動,點
的速度運動,點![]() 從
從![]() 開始沿
開始沿![]() 邊以
邊以![]() 的速度移動,如果點
的速度移動,如果點![]() 、
、![]() 分別從
分別從![]() 、
、![]() 同時出發,當其中一點到達
同時出發,當其中一點到達![]() 時,另一點也隨之停止運動,設運動時間為
時,另一點也隨之停止運動,設運動時間為![]() ,當
,當![]() ________時,四邊形
________時,四邊形![]() 也為矩形.
也為矩形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC 中,AB=AC,∠BAC=90,D、E 分別在 BC、AC 邊上,連接 AD、BE 相交于點 F,且∠CAD=![]() ∠ABE.
∠ABE.

(1)求證:BF=AC;
(2)如圖2,連接 CF,若 EF=EC,求∠CFD 的度數;
(3)如圖3,在⑵的條件下,若 AE=3,求 BF 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,該小組發現8米高旗桿DE的影子EF落在了包含一圓弧型小橋在內的路上,于是他們開展了測算小橋所在圖的半徑的活動。小剛身高1.6米,測得其影長為2.4米,同時測得EG的長為3米,HF的長為1米,測得拱高(弧GH的中點到弦GH的距離,即MN的長)為2米,求小橋所在圓的半徑。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】工藝美術中,常需設計對稱圖案.在如圖的正方形網格中,點![]() ,
,![]() 的坐標分別為
的坐標分別為![]() ,
,![]() .請在圖中再找一個格點
.請在圖中再找一個格點![]() ,使它與已知的
,使它與已知的![]() 個格點組成軸對稱圖形,則點
個格點組成軸對稱圖形,則點![]() 的坐標為________(如果滿足條件的點
的坐標為________(如果滿足條件的點![]() 不止一個,請將它們的坐標都寫出來).
不止一個,請將它們的坐標都寫出來).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(a,0),B(0,b),且|a+4|+b2﹣86+16=0.

(1)求a,b的值;
(2)如圖1,c為y軸負半軸上一點,連CA,過點C作CD⊥CA,使CD=CA,連BD.求證:∠CBD=45°;
(3)如圖2,若有一等腰Rt△BMN,∠BMN=90°,連AN,取AN中點P,連PM、PO.試探究PM和PO的關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com