
| 4 | 3 |
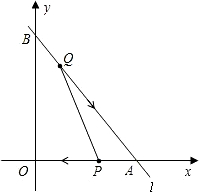 線段AO上以每秒1個單位長度的速度向點O移動,設點Q,P移動的時間為t秒
線段AO上以每秒1個單位長度的速度向點O移動,設點Q,P移動的時間為t秒| 30 |
| 11 |
| 30 |
| 11 |
| 36 |
| 11 |
| 50 |
| 13 |
| 50 |
| 13 |
| 100 |
| 13 |
| 28 |
| 13 |
| 28 |
| 13 |
| 4 |
| 3 |
| BO2+AO2 |
| PA |
| OA |
| QA |
| BA |
| t |
| 6 |
| 10-2t |
| 10 |
| 30 |
| 11 |
| PA |
| AB |
| AQ |
| AO |
| t |
| 10 |
| 10-2t |
| 6 |
| 50 |
| 13 |
| 30 |
| 11 |
| 50 |
| 13 |
| 30 |
| 11 |
| 30 |
| 11 |
| 36 |
| 11 |
| 36 |
| 11 |
| 36 |
| 11 |
| 50 |
| 13 |
| 50 |
| 13 |
| 100 |
| 13 |
| 28 |
| 13 |
| 28 |
| 13 |
| X |
| OA |
| BQ |
| BA |
| x |
| 6 |
| ||
| 10 |
| 60 |
| 13 |
| 60 |
| 13 |
| 4 |
| 3 |
| 60 |
| 13 |
| 24 |
| 13 |
| 60 |
| 13 |
| 24 |
| 13 |
|
|
| 3 |
| 4 |
| 21 |
| 13 |


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:
 如圖,已知直線l與坐標軸相交于點A(2,0)、B(0,-3).
如圖,已知直線l與坐標軸相交于點A(2,0)、B(0,-3).查看答案和解析>>
科目:初中數學 來源: 題型:
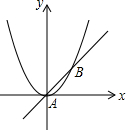 如圖,已知直線y=x與拋物線y=
如圖,已知直線y=x與拋物線y=| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
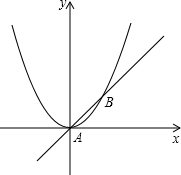 (2013•德宏州)如圖,已知直線y=x與拋物線y=
(2013•德宏州)如圖,已知直線y=x與拋物線y=| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2010•資陽)如圖,已知直線y=2x+2交y軸于點A,交x軸于點B,直線l:y=-3x+9
(2010•資陽)如圖,已知直線y=2x+2交y軸于點A,交x軸于點B,直線l:y=-3x+9| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
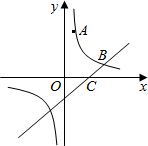 如圖,已知反比例函數的圖象經過點A,B,點A的坐標為(1,3),點B的縱坐標為1,點C的坐標為(2,0)
如圖,已知反比例函數的圖象經過點A,B,點A的坐標為(1,3),點B的縱坐標為1,點C的坐標為(2,0)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com