
【題目】為了“天更藍,水更綠”某市政府加大了對空氣污染的治理力度,經過幾年的努力,空氣質量明顯改善,現收集了該市連續(xù)30天的空氣質量情況作為樣本,整理并制作了如下表格和一幅不完整的條形統(tǒng)計圖:

說明:環(huán)境空氣質量指數(AQI)技術規(guī)定:ω≤50時,空氣質量為優(yōu);51≤ω≤100時,空氣質量為良;101≤ω≤150時,空氣質量為輕度污染;151≤ω≤200時,空氣質量為中度污染,…
根據上述信息,解答下列問題:
(1)直接寫出空氣污染指數這組數據的眾數 ,中位數 ;
(2)請補全空氣質量天數條形統(tǒng)計圖:
(3)根據已完成的條形統(tǒng)計圖,制作相應的扇形統(tǒng)計圖;
(4)健康專家溫馨提示:空氣污染指數在100以下適合做戶外運動,請根據以上信息,估計該市居民一年(以365天計)中有多少天適合做戶外運動?
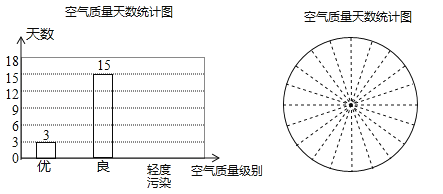
【答案】(1)90,90;(2)作圖見解析;(3)作圖見解析;(4)219.
【解析】
試題分析:(1)根據眾數的定義就可以得出這組數據的眾數為90,由30各數據中排在第15和第16兩個數的平均數就可以得出中位數為90;
(2)根據統(tǒng)計表的數據分別計算出,優(yōu)、良及輕度污染的時間即可;
(3)由條形統(tǒng)計圖分別計算出優(yōu)、良及輕度污染的百分比及圓心角的度數即可;
(4)先求出30天中空氣污染指數在100以下的比值,再由這個比值乘以365天就可以求出結論.
試題解析:(1)在這組數據中90出現的次數最多7次,故這組數據的眾數為90;在這組數據中排在最中間的兩個數是90,90,這兩個數的平均數是90,所以這組數據的中位數是90;
故答案為:90,90.
(2)由題意,得輕度污染的天數為:30﹣3﹣15=12天.
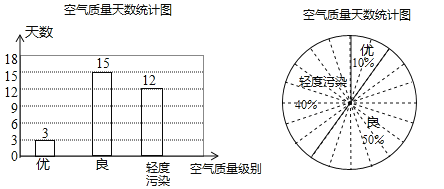
(3)由題意,得優(yōu)所占的圓心角的度數為:3÷30×360=36°,良所占的圓心角的度數為:15÷30×360=180°,輕度污染所占的圓心角的度數為:12÷30×360=144°.
(4)該市居民一年(以365天計)中有適合做戶外運動的天數為:18÷30×365=219天.


 名校名師培優(yōu)作業(yè)本加核心試卷系列答案
名校名師培優(yōu)作業(yè)本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中數學 來源: 題型:
【題目】以下五個命題:①對頂角相等;②內錯角相等;③同位角相等,兩直線平行;④0的立方根是0;⑤無限不循環(huán)小數是無理數.其中真命題的個數為( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:n=p×q(p,q是正整數,且p≤q),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p×q是n的最佳分解.并規(guī)定:F(n)=![]() .
.
例如12可以分解成1×12,2×6或3×4,因為12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=![]() .
.
(1)如果一個正整數m是另外一個正整數n的平方,我們稱正整數m是完全平方數.
求證:對任意一個完全平方數m,總有F(m)=1;
(2)如果一個兩位正整數t,t=10x+y(1≤x≤y≤9,x,y為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為36,那么我們稱這個數t為“吉祥數”,求所有“吉祥數”;
(3)在(2)所得“吉祥數”中,求F(t)的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【感知】如圖①,四邊形ABCD、CEFG均為正方形.可知BE=DG. 【拓展】如圖②,四邊形ABCD、CEFG均為菱形,且∠A=∠F.求證:BE=DG.
【應用】如圖③,四邊形ABCD、CEFG均為菱形,點E在邊AD上,點G在AD延長線上.若AE=2ED,∠A=∠F,△EBC的面積為8,則菱形CEFG的面積為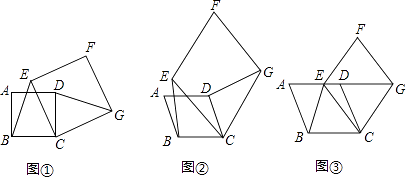
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某小區(qū)家庭用電情況,小明隨機調查了該小區(qū)n戶家庭2017年4月的用電量(用電量的數據都是整數),并將所得整數繪制成頻數分布直方圖如圖①所示. 
(1)求n的值,
(2)小明將所得數據按每戶用電量x(度)大小分為三檔,①低檔:121≤x≤160,②中檔:161≤x≤200,③高檔:201≤x≤240,并繪制成扇形統(tǒng)計圖如圖②所示,請幫助他將扇形統(tǒng)計圖補充完整.
(3)該地區(qū)對居民用電實行“階梯收費”,規(guī)定:用電量不超過200度按第一階梯電價收費,超過200度的部分按第二階梯電價收費,根據以上調查結果,估計2017年4月該小區(qū)300戶家庭僅按第一階梯電價收費額戶數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究
如圖,拋物線![]() 與
與![]() 軸交于A、B兩點(點A在點B的左側),與
軸交于A、B兩點(點A在點B的左側),與![]() 軸交于點C,連接AC、BC.點P沿AC以每秒1個單位長度的速度由點A向點C運動,同時,點Q沿BO以每秒2個單位長度的速度由點B向點O運動,當一個點停止運動時,另一個點也隨之停止運動,連接PQ,過點Q作QD⊥x軸,與拋物線交于點D,與BC交于點E.連接PD,與BC交于點F.設點P的運動時間為
軸交于點C,連接AC、BC.點P沿AC以每秒1個單位長度的速度由點A向點C運動,同時,點Q沿BO以每秒2個單位長度的速度由點B向點O運動,當一個點停止運動時,另一個點也隨之停止運動,連接PQ,過點Q作QD⊥x軸,與拋物線交于點D,與BC交于點E.連接PD,與BC交于點F.設點P的運動時間為![]() 秒(
秒(![]() ).
).
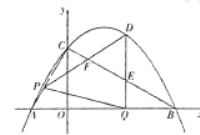
(1)求直線BC的函數表達式.
(2)①直接寫出P、D兩點的坐標(用含![]() 的代數式表示,結果需化簡).
的代數式表示,結果需化簡).
②在點P、Q運動的過程中,當PQ=PD時,求![]() 的值.
的值.
(3)試探究在點P、Q運動的過程中,是否存在某一時刻,使得點F為PD的中點.若存在,請直接寫出此時![]() 的值與點F的坐標;若不存在,請說明理由.
的值與點F的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com