
【題目】如圖,在 Rt△ABC 中,∠ABC=90°,AB=BC=![]() ,將△ABC 繞點 C 逆時針旋轉 60°,得到△MNC, 連接 BM,則 BM 的長是 .
,將△ABC 繞點 C 逆時針旋轉 60°,得到△MNC, 連接 BM,則 BM 的長是 .

【答案】![]() .
.
【解析】試題分析:首先考慮到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要構造直角三角形.由旋轉的性質可知,AC=AE,∠CAE=60°,故△ACE是等邊三角形,可證明△ABE與△CBE全等,可得到∠ABE=45°,∠AEB=30°,再證△AFB和△AFE是直角三角形,然后在根據勾股定理求解
解:連結CE,設BE與AC相交于點F,如下圖所示,
∵Rt△ABC中,AB=BC,∠ABC=90°
∴∠BCA=∠BAC=45°
∵Rt△ABC繞點A逆時針旋轉60°與Rt△ADE重合,
∴∠BAC=∠DAE=45°,AC=AE
又∵旋轉角為60°
∴∠BAD=∠CAE=60°,
∴△ACE是等邊三角形
∴AC=CE=AE=4
在△ABE與△CBE中,![]()
∴△ABE≌△CBE (SSS)
∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°
∴在△ABF中,∠BFA=180°﹣45°﹣45°=90°
∴∠AFB=∠AFE=90°
在Rt△ABF中,由勾股定理得,
BF=AF=![]() =2
=2
又在Rt△AFE中,∠AEF=30,°∠AFE=90°
FE=AF=2
∴BE=BF+FE=2+2
故,本題的答案是:2+2



科目:初中數學 來源: 題型:
【題目】教材中有如下一段文字:
思考
如圖,把一長一短的兩根木棍的一端固定在一起,擺出△ABC,固定住長木棍,轉動短木棍,得到△ABD,這個實驗說明了什么?
如圖中的△ABC與△ABD滿足兩邊和其中一邊的對角分別相等,即AB=AB,AC=AD,∠B=∠B,但△ABC與△ABD不全等.這說明,有兩邊和其中一邊的對角分別相等的兩個三角形不一定全等.
小明通過對上述問題的再思考,提出:兩邊分別相等且這兩邊中較大邊所對的角相等的兩個三角形全等.請你判斷小明的說法 . (填“正確”或“不正確”)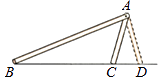
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題:
老舍先生曾說“天堂是什么樣子,我不曉得,但從我的生活經驗去判斷,北平之秋便是天堂.”(摘自《住的夢》)金黃色的銀杏葉為北京的秋增色不少.
小宇家附近新修了一段公路,他想給市政寫信,建議在路的兩邊種上銀杏樹.他先讓爸爸開車駛過這段公路,發現速度為60千米/小時,走了約3分鐘,由此估算這段路長約千米.
然后小宇查閱資料,得知銀杏為落葉大喬木,成年銀杏樹樹冠直徑可達8米.小宇計劃從路的起點開始,每a米種一棵樹,繪制示意圖如下:
考慮到投入資金的限制,他設計了另一種方案,將原計劃的a擴大一倍,則路的兩側共計減少200棵樹,請你求出a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年“五一”假期.某數學活動小組組織一次登山活動.他們從山腳下A點出發沿斜坡AB到達B點.再從B點沿斜坡BC到達山巔C點,路線如圖所示.斜坡AB的長為1040米,斜坡BC的長為400米,在C點測得B點的俯角為30°,點C到水平線AM的距離為600米.
(1)求B點到水平線AM的距離.
(2)求斜坡AB的坡度.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com