
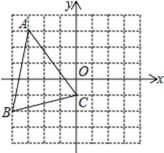
【題目】如圖,在下列帶有坐標系的網格中,△ABC的頂點都在邊長為1的小正方形的頂點上
(1) 直接寫出坐標:A__________,B__________
(2) 畫出△ABC關于y軸的對稱的△DEC(點D與點A對應)
(3) 用無刻度的直尺,運用全等的知識作出△ABC的高線BF(保留作圖痕跡)
 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:初中數學 來源: 題型:
【題目】已知,如圖:正方形ABCD,將Rt△EFG斜邊EG的中點與點A重合,直角頂點F落在正方形的AB邊上,Rt△EFG的兩直角邊分別交AB、AD邊于P、Q兩點,(點P與點F重合),如圖1所示:



(1)求證:EP2+GQ2=PQ2;
(2)若將Rt△EFG繞著點A逆時針旋轉α(0°<α≤90°),兩直角邊分別交AB、AD邊于P、Q兩點,如圖2所示:判斷四條線段EP、PF、FQ、QG之間是否存在什么確定的相等關系?若存在,證明你的結論.若不存在,請說明理由;
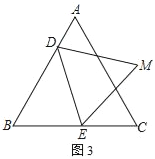
(3)若將Rt△EFG繞著點A逆時針旋轉α(90°<α<180°),兩直角邊所在的直線分別交BA、AD兩邊延長線于P、Q兩點,并判斷四條線段EP、PF、FQ、QG之間存在何種確定的相等關系?按題意完善圖3,請直接寫出你的結論(不用證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某辦公大樓正前方有一根高度是15米的旗桿ED,從辦公大樓頂端A測得旗桿頂端E的俯角α是45°,旗桿低端D到大樓前梯坎底邊的距離DC是20米,梯坎坡長BC是12米,梯坎坡度i=1: ![]() ,則大樓AB的高度為________米.
,則大樓AB的高度為________米.

查看答案和解析>>
科目:初中數學 來源: 題型:
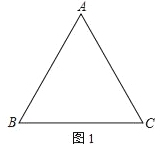
【題目】如圖,△ABC是邊長為6cm的等邊三角形,點D從B點出發沿B→A方向在線段BA上以a cm/s速度運動,與此同時,點E從線段BC的某個端點出發,以b cm/s速度在線段BC上運動,當D到達A點后,D、E運動停止,運動時間為t(秒).
(1)如圖1,若a=b=1,點E從C出發沿C→B方向運動,連AE、CD,AE、CD交于F,連BF.當0<t<6時:
①求∠AFC的度數;
②求![]() 的值;
的值;
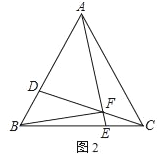
(2)如圖2,若a=1,b=2,點E從B點出發沿B→C方向運動,E點到達C點后再沿C→B方向運動.當t≥3時,連DE,以DE為邊作等邊△DEM,使M、B在DE兩側,求M點所經歷的路徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,函數y=![]() (k>0,x>0)的圖象經過菱形OACD的頂點D和邊AC的中點E,若菱形OACD的邊長為3,則k的值為_____.
(k>0,x>0)的圖象經過菱形OACD的頂點D和邊AC的中點E,若菱形OACD的邊長為3,則k的值為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是高,E、F分別是AB、AC的中點.

(1)AB=6,AC=4,求四邊形AEDF的周長;
(2)EF與AD有怎樣的位置關系?證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△AEC和△DFB中,∠E=∠F,點A,B,C,D在同一直線上,有如下三個關系式:①AE∥DF,②AB=CD,③CE=BF.

(1)請用其中兩個關系式作為條件,另一個作為結論,寫出你認為正確的所有命題(用序號寫出命題書寫形式:“如果,,那么”);
(2)選擇(1)中你寫出的一個命題,說明它正確的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠甲、乙兩車間接到加工一批零件的任務,從開始加工到完成這項任務共用了9天,乙車間在加工2天后停止加工,引入新設備后繼續加工,直到與甲車間同時完成這項任務為止,設甲、乙車間各自加工零件總數為y(件),與甲車間加工時間x(天),y與x之間的關系如圖(1)所示.由工廠統計數據可知,甲車間與乙車間加工零件總數之差z(件)與甲車間加工時間x(天)的關系如圖(2)所示.

(1)甲車間每天加工零件為_____件,圖中d值為_____.
(2)求出乙車間在引入新設備后加工零件的數量y與x之間的函數關系式.
(3)甲車間加工多長時間時,兩車間加工零件總數為1000件?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com